题目内容
8.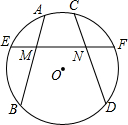 如图,弦AB,CD交EF于M,N,且ME=NF,∠AMN=∠CNM,求证:AB=CD.
如图,弦AB,CD交EF于M,N,且ME=NF,∠AMN=∠CNM,求证:AB=CD.
分析 作OP⊥EF于P,OQ⊥AB于Q,OR⊥CD于R,连结OM、ON,如图,根据垂径定理得PE=PF,则由ME=NF得到PM=PN,则可根据“SAS”判定△OPM≌△OPN,得到OM=ON,则根据等腰三角形的性质得∠OMN=∠ONM,由于∠AMN=∠CNM,所以∠OMQ=∠ONR,于是可根据“AAS”可判断△OMQ≌△ONR,得到OQ=OR,根据在同圆或等圆中,相等的弦心距所对应的弦相等得到AB=CD.
解答 证明:作OP⊥EF于P,OQ⊥AB于Q,OR⊥CD于R,连结OM、ON,如图,则PE=PF,
∵ME=NF,
∴PM=PN,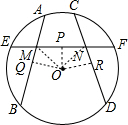
在△OPM和△OPN中,
$\left\{\begin{array}{l}{PM=PN}\\{∠OPM=∠OPN}\\{OP=OP}\end{array}\right.$,
∴△OPM≌△OPN,
∴OM=ON,
∴∠OMN=∠ONM,
∵∠AMN=∠CNM,
∴∠OMQ=∠ONR,
在△OMQ和△ONR中,
$\left\{\begin{array}{l}{∠OQM=∠ORN}\\{∠OMQ=∠ONR}\\{OM=ON}\end{array}\right.$,
∴△OMQ≌△ONR,
∴OQ=OR,
∴AB=CD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理和全等三角形的判定与性质.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
20.若多项式x2-2kx+4是一个完全平方式,则k的值是( )
| A. | 1 | B. | 2 | C. | ±1 | D. | ±2 |
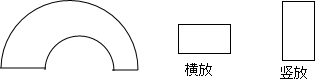 如图有一个拱形积木竖直放在地上,一块长方形积木横着,竖着都正好能卡进拱形门里,若长方形积木的长10厘米,宽6厘米,求拱形积木最高处离地面多少厘米?
如图有一个拱形积木竖直放在地上,一块长方形积木横着,竖着都正好能卡进拱形门里,若长方形积木的长10厘米,宽6厘米,求拱形积木最高处离地面多少厘米?