题目内容
3.若关于x的方程$\frac{{x}^{2}-bx}{ax-c}$=$\frac{m-1}{m+1}$有绝对值相同,符号相反的两个根,则m的值应为( )| A. | c | B. | $\frac{1}{c}$ | C. | $\frac{a-b}{a+b}$ | D. | $\frac{a+b}{a-b}$ |
分析 分式方程去分母整理后,根据方程有绝对值相同,符号相反的两个根,得到两根之和为0,即可求出m的值.
解答 解:去分母得:(x2-bx)(m+1)=(ax-c)(m-1),
整理得:(m+1)x2-b(m+1)x=amx-ax-cm+c,即(m+1)x2-(bm+b+a-am)x+cm-c=0,
由方程有绝对值相同,符号相反的两个根,得到$\frac{bm+b+a-am}{m+1}$=0,
整理得:m=$\frac{a+b}{a-b}$,
故选D
点评 此题考查了分式方程的解,解题的关键是理解“方程有绝对值相同,符号相反的两个根”即为两根之和为0.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
8.某珠宝店失窃,甲、乙、丙、丁四人涉嫌被拘审,四人的口供如下:甲:作案的是丙;乙:丁是作案者;丙:如果我作案,那么丁是主犯;丁:作案的不是我.如果四人口供中只有一个是假的,那么以下判断正确的是( )
| A. | 说假话的是甲,作案的是乙 | B. | 说假话的是丁,作案的是丙和丁 | ||
| C. | 假话的是乙,作案的是丙 | D. | 说假话的是丙,作案的是丙 |
 如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=$\frac{\sqrt{3}}{2}$.
如图,AB是⊙O的直径,C,D为⊙0上的两点,若∠CDB=30°,则∠ABC的度数为60°,cos∠ABC=$\frac{\sqrt{3}}{2}$.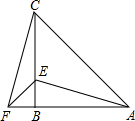 在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
在△ABC中,∠ACB=45°,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF