题目内容
10.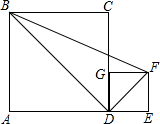 如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( )
如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( )| A. | 4.5 | B. | 3 | C. | 4 | D. | 2 |
分析 首先利用正方形的性质易得BD,DF,∠BDF=90°,利用直角三角形的面积公式得结果.
解答 解:∵四边形ABCD和四边形DEFG均为正方形,
∴BD=$\sqrt{2}AD$=3$\sqrt{2}$,DF=$\sqrt{2}DE$=$\sqrt{2}$,∠BDC=45°,∠GDF=45°,
∴∠BDF=90°,
∴S△BDF=$\frac{1}{2}DF•BD$=$\frac{1}{2}$×$\sqrt{2}×3\sqrt{2}$=3,
故选B.
点评 本题主要考查了正方形的性质,三角形的面积公式,利用正方形的性质得∠BDF=90°是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.小伟和小东是两个听话的好孩子,他们这学期的数学测试成绩见表一(单位:分).已知小伟平时成绩的平均分是98分,小东平时成绩的众数是93分.请结合图表完成下列问题:
(1)求表中的a和b;
(2)小伟和小东平时成绩谁更稳定?为什么?
(3)老师计划按表二的三张方案来折合计算两位同学本学期的数学总评成绩.请你选择一种方案帮老师计算两位同学本学期的数学总评成绩各是多少分?(注:算“平时成绩的权重”按“平时成绩的平均分的权重”来计算)
表一:
表二:
(1)求表中的a和b;
(2)小伟和小东平时成绩谁更稳定?为什么?
(3)老师计划按表二的三张方案来折合计算两位同学本学期的数学总评成绩.请你选择一种方案帮老师计算两位同学本学期的数学总评成绩各是多少分?(注:算“平时成绩的权重”按“平时成绩的平均分的权重”来计算)
表一:
| 测试类别 | 平时成绩 | 期中成绩 | 期末成绩 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 小伟 | a | 99 | 100 | 99 | 98 | 96 | 95 |
| 小东 | 90 | 93 | 94 | b | 95 | 92 | 98 |
| 测试类别 | 平时成绩的权重 | 期中成绩的权重 | 期末成绩的权重 |
| 方案一 | 10% | 30% | 60% |
| 方案二 | 20% | 20% | 60% |
| 方案三 | 20% | 30% | 50% |
15.如图所示,∠1和∠2是对顶角的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
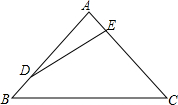 如图,在等腰三角形ABC中,AB=AC,∠A=80°,BC=12,点D、E分别在边AB、AC上,且DA=DE=EC,则EC=$4\sqrt{3}$.
如图,在等腰三角形ABC中,AB=AC,∠A=80°,BC=12,点D、E分别在边AB、AC上,且DA=DE=EC,则EC=$4\sqrt{3}$.
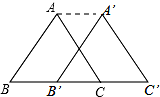 如图,已知△ABC的面积为16,BC的长为8,现将△ABC沿BC向右平移m个单位到△A′B′C′的位置.若四边形ABB′A′的面积为32,求m的值.
如图,已知△ABC的面积为16,BC的长为8,现将△ABC沿BC向右平移m个单位到△A′B′C′的位置.若四边形ABB′A′的面积为32,求m的值.