题目内容
2.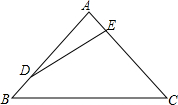 如图,在等腰三角形ABC中,AB=AC,∠A=80°,BC=12,点D、E分别在边AB、AC上,且DA=DE=EC,则EC=$4\sqrt{3}$.
如图,在等腰三角形ABC中,AB=AC,∠A=80°,BC=12,点D、E分别在边AB、AC上,且DA=DE=EC,则EC=$4\sqrt{3}$.
分析 过点B作BF∥DE,过点E作EF∥AB,EF与BF交于点F,连接CF,过点F作FG⊥BC于点G,构建平行四边形BDEF,得到BF=DE,BD=EF,证明△ADE≌△ECF,得到FC=DE,进而得到FC=CE=BF,求出∠FBC=∠ABC-∠DBF=50°-20°=30°,利用等腰三角形的性质得到BG=CG=6,利用含30°的直角三角形的性质和勾股定理,即可解答.
解答 解:如图,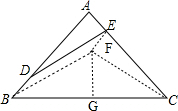
过点B作BF∥DE,过点E作EF∥AB,EF与BF交于点F,连接CF,过点F作FG⊥BC于点G,
∴四边形BDEF是平行四边形,
∴BF=DE,BD=EF,
∵DA=DE,∠A=80°,
∴∠AED=80°,∠ADE=180°-80°-80°=20°,
∵BF∥DE,
∴∠DBF=∠ADE=20°,
∴∠DEF=∠DBF=20°,
∴∠CEF=180°-∠AED-∠DEF=180°-80°-20°=80°,
∴∠CEF=∠A,
∵AB=AC,DA=EC,
∴BD=AE,
∴EF=AE,
在△ADE和△ECF中,
$\left\{\begin{array}{l}{EC=DA}\\{∠A=∠CEF}\\{AE=EF}\end{array}\right.$
∴△ADE≌△ECF,
∴FC=DE,
∵DE=BF=CE,
∴FC=CE=BF,
∵AB=AC,∠A=80°,
∴∠ABC=(180°-∠A)÷2=50°,
∴∠FBC=∠ABC-∠DBF=50°-20°=30°,
∵FG⊥BC,BF=CF,AB=12,
∴BG=CG=$\frac{1}{2}$AB=6,
在Rt△BGF中,∠FBC=30°,
∴BF=2FG,
根据勾股定理得,BF2-FG2=BG2,
∴4FG2-FG2=36,
∴FG=2$\sqrt{3}$,
∴BF=4$\sqrt{3}$,
∴EC=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了等腰三角形的性质、平行四边形的性质与判定,含30°的直角三角形的性质,勾股定理,解决本题的关键是作出辅助线,构建平行四边形.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| y | 50 | 80 | 100 | 150 | … |
| x | 30 | 45 | 55 | 80 | … |
| A. | y=2x-10 | B. | y=x2 | C. | y=x+25 | D. | y=x+5 |
| A. | 某射击运动员射一次,正中靶心 | |
| B. | 下雨后,天空出现彩虹 | |
| C. | 测量抚州市某天的气温是-100℃ | |
| D. | 口袋中装有1个黑球和2个白球,从中摸出2个球,其中必有白球 |
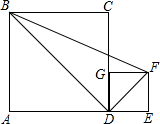 如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( )
如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( ) 如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°.
如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°. 如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
如图,直线l1的解析式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.