题目内容
5.(1)计算:(-1)2015+($\frac{1}{2}$)-2(2)先化简,再求值:(12ab3-8a2b2)+(-4ab)+(2a-3b)(a+b),其中a=2,b=1.
(3)已知x2-5x-14=0,求(x-1)(2x-1)-(x+1)2+1的值.
分析 (1)原式第一项利用乘方的意义化简,第二项利用负整数指数幂法则计算即可得到结果;
(2)原式利用多项式除以单项式,以及多项式乘以多项式法则计算,去括号合并得到最简结果,把a与b的值代入计算即可求出值;
(3)原式利用多项式乘以多项式,以及完全平方公式化简,去括号合并后将已知等式变形后代入计算即可求出值.
解答 解:(1)原式=-1+4=3;
(2)原式=-3b2+2ab+2a2+2ab-3ab-3b2=2a2-6b2+ab,
当a=2,b=1时,原式=8-6+2=4;
(3)原式=2x2-x-2x+1-x2-2x-1+1=x2-5x+1,
由x2-5x-14=0,得到x2-5x=14,
则原式=15.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
15.边长为5cm的菱形的周长是( )
| A. | 10cm | B. | 15cm | C. | 20cm | D. | 25cm |
16.把分式$\frac{1}{x-y}$,$\frac{1}{x+y}$,$\frac{1}{{x}^{2}-{y}^{2}}$进行通分,它们的最简公分母是( )
| A. | x-y | B. | x+y | C. | x2-y2 | D. | (x+y)(x-y)(x2-y2) |
20.下列运算正确的是( )
| A. | (x2)3=x5 | B. | m5÷m2=m3 | C. | (a-b)2=a2-b2 | D. | m2•m3=m6 |
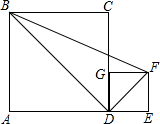 如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( )
如图:A,D,E在同一条直线上,AD=3,DE=1,BD,DF分别为正方形ABCD,正方形DEFG的对角线,则三角形△BDF的面积为( ) 如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°.
如图,已知CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠CAE=55°,则∠ACE=70°. 如图,已知∠1=∠2,∠3=100°,则∠4=80°.
如图,已知∠1=∠2,∠3=100°,则∠4=80°.