题目内容
10.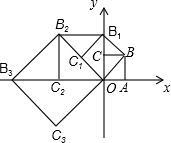 如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).
如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).
分析 首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标之间的规律,然后根据规律计算出点B2015的坐标.
解答 解:∵正方形OABC边长为1,
∴OB=$\sqrt{2}$,
∵正方形OBB1C1是正方形OABC的对角线OB为边,
∴OB1=2,
∴B1点坐标为(0,2),
同理可知OB2=2$\sqrt{2}$,B2点坐标为(-2,2),
同理可知OB3=4,B3点坐标为(-4,0),
B4点坐标为(-4,-4),B5点坐标为(0,-8),
B6(8,-8),B7(16,0)
B8(16,16),B9(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,
∵2015÷8=251…7,
∴B2015的纵横坐标符号与点B7的相同,横坐标为正值,纵坐标是0,
∴B2015的坐标为(21008,0).
故答案为:(21008,0).
点评 本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的$\sqrt{2}$倍,此题难度较大.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
2.-1.5的倒数是( )
| A. | 0 | B. | -1.5 | C. | 1.5 | D. | -$\frac{2}{3}$ |
19.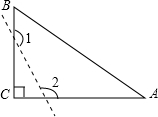 如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
 如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,已知△ABC中,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 270° | D. | 315° |
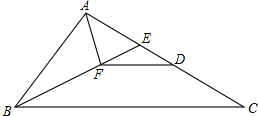 推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.
推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.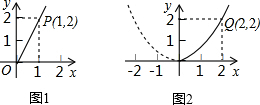
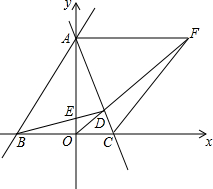 如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.
如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.