题目内容
1.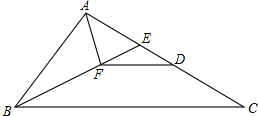 推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.
推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.解:∵FD∥BC
∴∠ADF=∠C两直线平行,同位角相等,
∵∠ABF=∠C
∴∠ABF=∠ADF等量代换
∵AF平分∠BAE
∴∠BAF=∠CAF(角平分线的定义)
在△BAF和△DAF中
$\left\{\begin{array}{l}{∠BAF=∠DAF}\\{∠ABF=∠ADF}\\{\;}\end{array}\right.$
AF=AF
∴△BAF≌△DAFAAS
∴AB=AD
∵AC-AD=DC
∴AC-AB=DC.
分析 根据题意正确填上根据和条件即可.
解答 解:∵FD∥BC,
∴∠ADF=∠C,(两直线平行,同位角相等.)
∵∠ABF=∠C,
∴∠ABF=∠ADF,(等量代换)
∵AF平分∠BAE,
∴∠BAF=∠CAF,(角平分线的定义)
在△BAF和△DAF中$\left\{\begin{array}{l}{∠BAF=∠DAF}\\{∠ABF=∠ADF}\\{AF=AF}\end{array}\right.$,
∴△BAF≌△DAF(AAS)
∴AB=AD,
∵AC-AD=DC,
∴AC-AB=DC.
故答案为:两直线平行,同位角相等,等量代换,∠BAF=∠CAF,AF=AF,AAS.
点评 本题考查了平行线的性质,等量代换,角平分线的定义,全等三角形的判定与性质,熟记定理是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
12.在平面直角坐标系中,各点的坐标分别为A1(1、3)、A2(2、5)、A3(3、7)、A4(4、9)、A5(5、11)、A6(6、13)…用你发现的规律确定A2014的坐标(2014,4029).
9.统计得到一组数据,其中最大值是132,最小值是50,取组距为10,可以分成( )
| A. | 10组 | B. | 9组 | C. | 8组 | D. | 7组 |
 如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.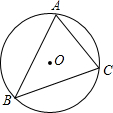 如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB=$\frac{2}{3}$.
如图,已知△ABC的外接圆O的半径为3,AC=4,则sinB=$\frac{2}{3}$.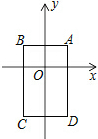 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).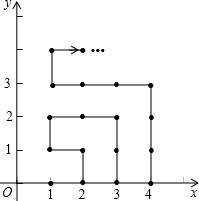 在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少?
在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少?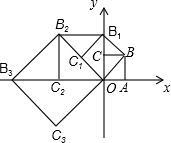 如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).
如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0). 如图,在△ABC中,AB=AC,D是BC的中点.AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A,E两点,交AB于点F.已知BC=16$\sqrt{2}$,AD=4.
如图,在△ABC中,AB=AC,D是BC的中点.AE平分∠BAD交BC于点E,点O是AB上一点,⊙O过A,E两点,交AB于点F.已知BC=16$\sqrt{2}$,AD=4.