题目内容
8. 如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.
如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=20°,则∠AOB=80°.
分析 两次利用角平分线的性质计算即可求解.
解答 解:∵OC是∠AOB的平分线,
∴∠AOC=∠COB;
∵OD是∠AOC的平分线,
∴∠AOD=∠COD;
∵∠COD=20°,
∴∠AOC=40°,
∴∠AOB=80°.
故答案为:80°.
点评 本题考查了角的平分线的性质,关键是熟悉角平分线的性质是将两个角分成相等的两个角的知识点.

练习册系列答案
相关题目
19.计算:
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
(1)($\sqrt{3}-1$)0+|-3|-($\frac{1}{2}$)-2+$\sqrt{4}$
(2)$\frac{{x}^{2}}{x-2}$+$\frac{4}{2-x}$.
16.在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
(1)表中a的值等于0.25;
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 |
| 摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
| 摸到黑球的频率 $\frac{m}{n}$ | 0.26 | 0.247 | 0.245 | 0.248 | a |
(2)估算口袋中白球的个数;
(3)用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
13.已知点M(-1,5)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (5,-1) | B. | (-1,-5) | C. | (1,5) | D. | (5,1) |
20. 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )
 如图,图中共有同旁内角( )
如图,图中共有同旁内角( )| A. | 4对 | B. | 5对 | C. | 6对 | D. | 7对 |
18.下列各式由左边到右边的变形中,是分解因式的为( )
| A. | a (x+y)=a x+a y | B. | x2-4x+4=x(x-4)+4 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+3x=(x-4)(x+4)+3x |
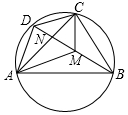 已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证:
已知圆内接四边形ABCD的对角线AC、BD交于N点,M在BD上,且∠DAN=∠BAM,∠DCN=∠BCM.求证: