题目内容
13.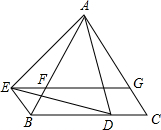 已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.
已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.(1)求证:△AEB≌△ADC;
(2)判断并证明四边形BCGE的形状.
分析 (1)由△ABC和△ADE都是等边三角形,所以AB=AC,AE=AD,∠BAC=∠EAD=∠C=60°,所以∠EAB=∠DAC由此可以对称结论.
(2)欲证明四边形BCGE是平行四边形只要证明EB∥CG,只要证明∠BEF=60°,∠CGE=120°即可.
解答  (1)证明:∵△ABC和△ADE都是等边三角形,
(1)证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=∠C=60°,
∴∠EAB=∠DAC,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AE=AD}\\{∠EAB=∠CAD}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACD,
(2)结论四边形BCGE是平行四边形,
证明:∵△ABE≌△ACD,∠ABC=∠C=60°
∴∠ABE=∠C=60°,
∵EG∥BC,
∴∠EFB=∠ABC=60°,∠C+∠EGC=120°
∴△EFB是等边三角形,∠EGC=120°
∴∠BEF=60°,
∴∠BEF+∠CGE=180°,
∴BE∥CG,
∵EG∥BC,
∴四边形EBCG是平行四边形.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、平行四边形的判定,熟练掌握全等三角形的判定方法是解决问题的关键,需要记住平行四边形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
18.若a<b,则下列不等式的变形中不正确的是( )
| A. | a+5<b+5 | B. | $\frac{a}{5}$$<\frac{b}{5}$ | C. | 5a-1<5b-1 | D. | 5-a<5-b |
3.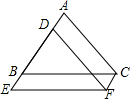 如图,将△ABC沿AB方向平移2cm得到△DEF,已知△ABC的周长为22cm,则四边形AEFC的周长为( )
如图,将△ABC沿AB方向平移2cm得到△DEF,已知△ABC的周长为22cm,则四边形AEFC的周长为( )
 如图,将△ABC沿AB方向平移2cm得到△DEF,已知△ABC的周长为22cm,则四边形AEFC的周长为( )
如图,将△ABC沿AB方向平移2cm得到△DEF,已知△ABC的周长为22cm,则四边形AEFC的周长为( )| A. | 26cm | B. | 24cm | C. | 22cm | D. | 20cm |
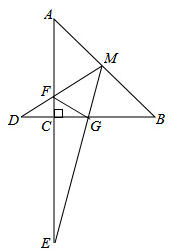 如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°.
如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°. 作图题
作图题