题目内容
1.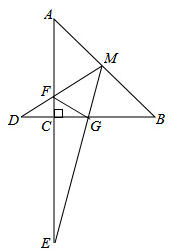 如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°.
如图,M为等腰直角三角形ABC斜边AB的中点,AC=4,MD交AC于F,交BC延长线于D,ME交BC于G,交AC延长线于E,且AF=3,∠DMG=45°.(1)写出图中的三对相似三角形.
(2)连接FG,求FG的长.
分析 (1)等腰三角形的性质以及三角形外角的性质求得两组相等的角,即可判定三角形相似;
(2)根据△AMF∽△BGM,对应边成比例求得BG,进而求得CG,然后根据勾股定理即可求得FG.
解答 解:(1)∵△ABC是等腰直角三角形,
∴∠A=∠B=45°,
∵∠DMG=45°,
∴∠D=∠DMG,
∵∠DGM=45°+∠BMG=∠DMB,
∴△DMG∽△DBM,
∵∠A=∠EMF=45°,∠AMF=45°+∠AMF=∠MFE,
∴△EMF∽△EAM,
∵∠A=∠B=45°,∠DGM=∠DMB,
∴∠MGB=∠AMF,
∴△AMF∽△BGM;
故相似的三角形有:△DMG∽△DBM,△EMF∽△EAM,△AMF∽△BGM;
(2)∵AC=4,AF=3,
∴AB=4$\sqrt{2}$,CF=4-3=1,
∵M为等腰直角三角形ABC斜边AB的中点,
∴AM=BM=2$\sqrt{2}$,
∵△AMF∽△BGM,
∴$\frac{BG}{AM}$=$\frac{BM}{AF}$,
∴BG=$\frac{2\sqrt{2}×2\sqrt{2}}{3}$=$\frac{8}{3}$,
∴CG=4-$\frac{8}{3}$=$\frac{4}{3}$,
在RT△FCG中,FG=$\sqrt{C{F}^{2}+C{G}^{2}}$=$\frac{5}{3}$.
点评 本题考查了等腰直角三角形的性质,相似三角形的判定和性质,勾股定理的应用等,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
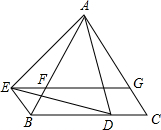 已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.
已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.