题目内容
5.若代数式-2a2+3a+18=8,则二次根式$\sqrt{6{a}^{2}-9a+2}$的最简结果为4$\sqrt{2}$.分析 首先化简已知代数式,进而代入二次根式求出答案.
解答 解:∵-2a2+3a+18=8,
∴2a2-3a=10,
∴$\sqrt{6{a}^{2}-9a+2}$=$\sqrt{3(2{a}^{2}-3a)+2}$=$\sqrt{32}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 此题主要考查了二次根式的性质与化简,利用整体思想解题是解题关键.

练习册系列答案
相关题目
20.对于任意两个实数对(a,b),和(c,d),当且仅当a=c且b=d时,(a,b)=(c,d).我们现在定义新运算“※”:(a,b)※(c,d)=(a2-c,b+d2).若(2,x)※(y,5)=(3,34),则xy的值为( )
| A. | 3 | B. | -3 | C. | 9 | D. | -9 |
17.$\sqrt{8n}$是整数,正整数n的最小值是( )
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
15.下列命题中,属于假命题的是( )
| A. | 如果a>b,那么-a<-b | |
| B. | 等角的余角相等 | |
| C. | 等式的两边同加上或同减去一个式子,结果仍为等式 | |
| D. | 如果a+b>0,那么a>0,b>0 |
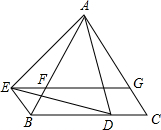 已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.
已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.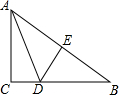 如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )
如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )