题目内容
2.将函数y=x2的图象向右平移2个单位得函数y1的图象,将y与y1合起来构成新图象,直线y=m被新图象依次截得三段的长相等,则$\frac{1}{4}$或4.分析 根据“左加右减”的原则求出与y1的函数解析式,然后求得新图象与直线的交点横坐标,根据截得三段的长相等,分两种情况列出方程,解方程即可求得.
解答 解:∵二次函数y=x2的图象向右平移2个单位,
∴平移后的解析式为:y=(x-2)2,
把y=m代入y=x2得m=x2,解得x=±$\sqrt{m}$,
把y=m代入y=(x-2)2得m=(x-2)2,解得x=2±$\sqrt{m}$,
当0<m<1时,则$\sqrt{m}$-(-$\sqrt{m}$)=2-$\sqrt{m}$-$\sqrt{m}$,解得m=$\frac{1}{4}$,
当m>1时,则2+$\sqrt{m}$-$\sqrt{m}$=$\sqrt{m}$-(2-$\sqrt{m}$),解得m=4,
故答案为$\frac{1}{4}$或4.
点评 本题考查的是一次函数的图象与几何变换,熟知“上加下减,左加右减”的原则是解答此题的关键.

练习册系列答案
相关题目
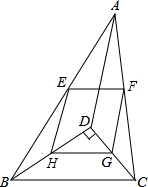 如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.
如图,点D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,点E,F,G,H分别是线段AB,AC,CD,BD的中点.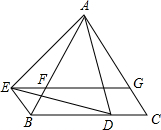 已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.
已知:如图,△ABC是等边三角形,点D在线段BC上(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,EG∥BC,连接BE.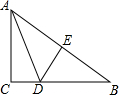 如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )
如图,已知直角三角形ABC中,∠C=90°,BC=8,AB的垂直平分线DE交BC于点D,AD=5,则AC的长为( )