题目内容
4. 如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是( )
如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是( )| A. | ∠BAD=∠CAD | B. | ∠BED=∠CED | C. | BE=CE | D. | AE=DE |
分析 由△ADB≌△ADC,推出∠BAD=∠CAD,∠BDE=∠CDE,由△EDC≌△EDB,推出BE=EC,∠BED=∠CED,即可判断.
解答 解:在△ADB和△ADC中,
$\left\{\begin{array}{l}{AC=AB}\\{AD=AD}\\{CD=BD}\end{array}\right.$,
∴△ADB≌△ADC,
∴∠BAD=∠CAD,∠BDE=∠CDE,
在△EDC和△EDB中,
$\left\{\begin{array}{l}{ED=ED}\\{∠EDB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△EDC≌△EDB,
∴BE=EC,∠BED=∠CED,
故A、B、C正确,
故选D.
点评 本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
12.对于任意有理数a,b,现用★定义一种运算:a★b=a2-b2.根据这个定义,代数式(x+y)★y可以化简为( )
| A. | xy+x2 | B. | xy-y2 | C. | x2+2xy | D. | x2 |
14. 如图,BD∥CE,∠1=85°,∠2=37°,则∠A的度数是( )
如图,BD∥CE,∠1=85°,∠2=37°,则∠A的度数是( )
 如图,BD∥CE,∠1=85°,∠2=37°,则∠A的度数是( )
如图,BD∥CE,∠1=85°,∠2=37°,则∠A的度数是( )| A. | 15度 | B. | 37度 | C. | 48度 | D. | 53度 |
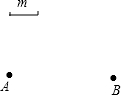 如图,已知平面内A,B两点和线段m.
如图,已知平面内A,B两点和线段m.