题目内容
9.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,商场经调查发现,如果每件衬衫降价1元,商场平均每天可多售出2件,若商场平均每天想盈利1200元,是否可能,若可能则每件衬衫应降价多少元?分析 由题意,可设衬衫的单价应下降x元.则每天可售出(20+2x)件,每件盈利(40-x)元.再根据相等关系:每天的获利=每天售出的件数×每件的盈利;列方程求解即可.
解答 解:设每件应降价x元,根据题意,
得 (40-x)(20+2x)=1200.
解这个方程,得 x1=10,x2=20,
∵为了扩大销售,
∴x取20.
答:每件衬衫应降价20元.
点评 考查了一元二次方程的应用,找到题目的相等关系:每天的获利=每天售出的件数×每件的盈利;是解答本题的关键,注意判断所求的解是否符合题意.

练习册系列答案
相关题目
2.解关于x的不等式组$\left\{\begin{array}{l}{x-a<0}\\{7-2x≤2}\end{array}\right.$的整数解有4个,则a的取值范围是( )
| A. | 6<a<7 | B. | 6≤a<7 | C. | 6≤a≤7 | D. | 6<a≤7 |
17.甲、乙两个学习小组各有4名同学,在某次测验中,他们的得分情况如下表所示:
设两组同学得分的平均数依次为X甲、X乙,得分的方差依次为S2甲、S2乙,则下列关系中完全正确的是( )
| 组员1 | 组员2 | 组员3 | 组员4 | |
| 甲 | 88 | 95 | 97 | 100 |
| 乙 | 90 | 94 | 97 | 99 |
| A. | X甲=X乙,S2甲>S2乙 | B. | X甲=X乙,S2甲<S2乙 | ||
| C. | X甲<X乙,S2甲>S2乙 | D. | X甲<X乙,S2甲<S2乙 |
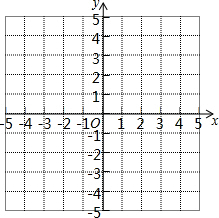 如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(-1,-2),B(1,1),C(-3,1),△A1B1C1是△ABC向下平移2个单位,向右平移3个单位得到的.
如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(-1,-2),B(1,1),C(-3,1),△A1B1C1是△ABC向下平移2个单位,向右平移3个单位得到的.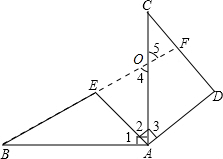 如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.
如图,∠BAC=∠DAE=90°,AC=AB,AE=AD,试说明BE⊥CD.