��Ŀ����
2����֪����x��һԪ���η���x2-��m+1��x+$\frac{1}{2}$��m2+1��=0��ʵ��������1����m��ֵ��
��2������y=x2-��m+1��x+$\frac{1}{2}$��m2+1����ͼ�����x��ĶԳ�ͼ�Σ�Ȼ������ͼ������ƽ��3����λ���ȣ�������ƽ��2����λ���ȣ�д���仯��ͼ��Ľ���ʽ��
��3���ڣ�2���������£���ֱ��y=2x+n��n��m����仯���ͼ���й�����ʱ����n2-4n�����ֵ����Сֵ��
���� ��1�����������0���г�����ʽ���ⲻ��ʽ���ɣ�
��2���������ۣ�ƽ�ƺ��ͼ���ݶ������꼴��д�������Ľ���ʽ��
��3������ȷ��n��ȡֵ��Χ�����ö��κ��������ʼ��ɽ�����⣻
��� �⣺��1������һԪ���η���x2-��m+1��x+$\frac{1}{2}$��m2+1��=0��
��=��m+1��2-2��m2+1��=-m2+2m-1=-��m-1��2��
�߷�����ʵ������
��-��m-1��2��0��
��m=1��
��2���ɣ�1����֪y=x2-2x+1=��x-1��2��
ͼ����ͼ��ʾ��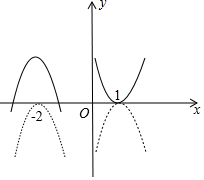
ƽ�ƺ�Ľ���ʽΪy=-��x+2��2+2=-x2-4x-2��
��3����$\left\{\begin{array}{l}{y=2x+n}\\{y=-{x}^{2}-4x-2}\end{array}\right.$��ȥy�õ�x2+6x+n+2=0��
���������0��
��36-4n-8��0��
��n��7��
��n��m��m=1��
��1��n��7��
��y��=n2-4n=��n-2��2-4��
��n=2ʱ��y���ֵ��С����СֵΪ-4��
n=7ʱ��y���ֵ������ֵΪ21��
��n2-4n�����ֵΪ21����СֵΪ-4��
���� ���⿼����������x��Ľ��㡢����ϵ���������۱任��ƽ�Ʊ任�����κ�������ֵ�����֪ʶ������Ĺؼ����������⣬ѧ����ת����˼��˼�����⣬�����п��������ͣ�

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�| A�� | 140��x��150 |
| B�� | 130��x��140 |
| C�� | 120��x��130 |
| D�� | 110��x��120 |
| E�� | 100��x��110 |
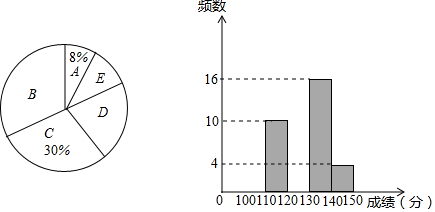
��1��m��ֵΪ50������ͳ��ͼ��D���Ӧ��Բ�Ľ���72�㣮
��2����Ҫ�ӳɼ������ѧ���ס��ҡ��������У����ѡ��2�˽��ܾ��飬��ס���������������1�˱�ѡ�еĸ��ʣ�ͨ������״ͼ���б������з�������
| A�� | x��2 | B�� | x��2 | C�� | x=-1 | D�� | x=2 |