题目内容
19. 如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.
如图,四边形ABCD为平行四边形,AE平分∠BAD交BC于点E,过点E作EF∥AB,交AD于点F,连接BF.(1)求证:BF平分∠ABC;
(2)若AB=6,且四边形ABCD∽四边形CEFD,求BC长.
分析 (1)首先证明四边形ABEF是平行四边形,再由平行线的性质和角平分线证出∠BAE=∠AEB,证出AB=EB,得出四边形ABEF是菱形,即可得出结论;
(2)由相似多边形的性质得出对应边成比例,即可得出BC的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠FAE=∠AEB,
∵EF∥AB,
∴四边形ABEF是平行四边形,
∵AE平分∠BAD,
∴∠FAE=∠BAE,
∴∠BAE=∠AEB,
∴AB=EB,
∴四边形ABEF是菱形,
∴BF平分∠ABC;
(2)解:∵四边形ABEF为菱形;
∴BE=AB=6,
∵四边形ABCD∽四边形CEFD,
∴$\frac{AB}{CE}=\frac{BC}{CD}$,即$\frac{6}{BC-6}=\frac{BC}{6}$,
解得:BC=3±3$\sqrt{5}$(负值舍去),
∴BC=3+3$\sqrt{5}$.
点评 本题考查了菱形的判定与性质、相似多边形的性质、平行四边形的判定与性质、等腰三角形的判定;熟练掌握平行四边形的判定与性质,证明四边形ABEF是菱形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.下列方差最大的一组数据是( )
| A. | 6,6,6,6,6 | B. | 5,6,6,6,7 | C. | 4,5,6,7,8 | D. | 3,3,6,9,9 |
7.中考前的模拟考试对于学生来说具有重大的指导意义,现抽取m名学生的数学一模成绩进行整理分组,形成如下表格(x代表成绩,规定x>140为优秀),并绘制出扇形统计图和频数分布直方图(横坐标表示成绩,单位:分).
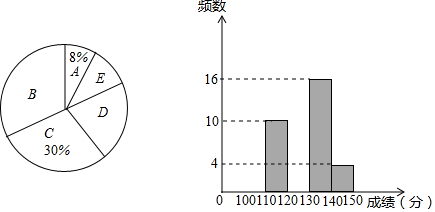
(1)m的值为50;扇形统计图中D组对应的圆心角是72°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).
| A组 | 140<x≤150 |
| B组 | 130<x≤140 |
| C组 | 120<x≤130 |
| D组 | 110<x≤120 |
| E组 | 100<x≤110 |

(1)m的值为50;扇形统计图中D组对应的圆心角是72°.
(2)若要从成绩优秀的学生甲、乙、丙、丁中,随机选出2人介绍经验,求甲、乙两人中至少有1人被选中的概率(通过画树状图或列表法进行分析).
9. 如图是一个正六棱柱的茶叶盒,其俯视图为( )
如图是一个正六棱柱的茶叶盒,其俯视图为( )
 如图是一个正六棱柱的茶叶盒,其俯视图为( )
如图是一个正六棱柱的茶叶盒,其俯视图为( )| A. |  | B. |  | C. |  | D. |  |
 已知关于x的不等式3x+mx>-8的解集如图所示,则m的值为1.
已知关于x的不等式3x+mx>-8的解集如图所示,则m的值为1.