Question

3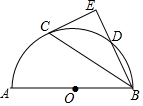．如图，点D是以AB为直径的半圆O上一点，连接BD，点C是$\widehat{AD}$的中点，过点C作直线BD的垂线，垂足为点E．
求证：（1）CE是半圆O的切线；
           （2）BC²=AB•BE．

Answer 1

分析 （1）连接OC，根据圆周角定理得到∠ABC=∠DBC，根据等腰三角形的性质得到∠OCB=∠OBC，等量代换得到∠OCB=∠CBD，推出OC∥BD，根据平行线的性质得到OC⊥CE，于是得到结论；
（2）连接AC，由AB是⊙O的直径，得到∠ACB=90°，根据相似三角形的性质即可得到结论．

解答 证明：（1）连接OC，
∵点C是$\widehat{AD}$的中点，
∴$\widehat{AC}$=$\widehat{CD}$，
∴∠ABC=∠DBC，
∵OC=OB，
∴∠OCB=∠OBC，
∴∠OCB=∠CBD，
∴OC∥BD，
∵CE⊥BE，
∴OC⊥CE，
∴CE是半圆O的切线；

（2）连接AC，
∵AB是⊙O的直径，
∴∠ACB=90°，
∵CE⊥BE，
∴∠E=90°，
∴∠E=∠ACB，
∵∠ABC=∠CBD，
∴△ABC∽△CBE，
∴$\frac{AB}{BC}=\frac{BC}{BE}$，
∴BC²=AB•BE．

点评 本题考查了相似三角形的判定和性质，切线的判定，圆周角定理，正确的作出辅助线是解题的关键．