题目内容
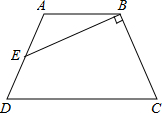 如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是
如图,已知等腰梯形ABCD中,AB∥CD,AB=2,CD=4,AD=BC,E是AD的中点,EB⊥BC,则梯形ABCD的面积是考点:等腰梯形的性质
专题:
分析:先延长CD交BE延长线上点G,过点A作AM⊥DC,过点B作BH⊥DC,根据AB∥CD,E是AD的中点得出△AEB≌△DEG,再根据AB=2,得出DG和GC的长,再根据ABCD是等腰梯形,AM⊥DC,BH⊥DC,得出DM=HC的值,再根据EB⊥BC,BH⊥DC得出△BGC∽△HBC,从而得出BC和BG的值,即可求出S△BGC的值,再根据△AEB≌△DEG,即可得出梯形ABCD的面积.
解答: 解:延长CD交BE延长线上点G,过点A作AM⊥DC,过点B作BH⊥DC,
解:延长CD交BE延长线上点G,过点A作AM⊥DC,过点B作BH⊥DC,
∵AB∥CD,
∴∠GDE=∠EAB,
∵E是AD的中点,
∴AE=ED,
∵∠GED=∠AEB,
∴△AEB≌△DEG,
∵AB=2,
∴DG=2,
∴GC=CD+GD=4+2=6,
∵AM⊥DC,BH⊥DC,AD=BC,
∴DM=HC=1,
∵EB⊥BC,BH⊥DC,
∴∠EBC=∠BHC=90°,
∵∠C=∠C,
∴△BGC∽△HBC,
∴
=
,
∴BC2=GC•HC,
∴BC=
=
,
∴BG2=GC2-BC2,
∴BG=
=
,
∴S△BGC=
•BC•BG=
×
×
=3
,
∵△AEB≌△DEG,
∴梯形ABCD与三角形BGC的面积相等,
∴S梯形ABCD=3
;
故答案为:3
.
 解:延长CD交BE延长线上点G,过点A作AM⊥DC,过点B作BH⊥DC,
解:延长CD交BE延长线上点G,过点A作AM⊥DC,过点B作BH⊥DC,∵AB∥CD,
∴∠GDE=∠EAB,
∵E是AD的中点,
∴AE=ED,
∵∠GED=∠AEB,
∴△AEB≌△DEG,
∵AB=2,
∴DG=2,
∴GC=CD+GD=4+2=6,
∵AM⊥DC,BH⊥DC,AD=BC,
∴DM=HC=1,
∵EB⊥BC,BH⊥DC,
∴∠EBC=∠BHC=90°,
∵∠C=∠C,
∴△BGC∽△HBC,
∴
| GC |
| BC |
| BC |
| HC |
∴BC2=GC•HC,
∴BC=
| 6×1 |
| 6 |
∴BG2=GC2-BC2,
∴BG=
62-
|
| 30 |
∴S△BGC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 30 |
| 5 |
∵△AEB≌△DEG,
∴梯形ABCD与三角形BGC的面积相等,
∴S梯形ABCD=3
| 5 |
故答案为:3
| 5 |
点评:此题考查了等腰梯形的性质,本题通过作辅助线,把等腰梯形ABCD的面积转化为三角形BGC的面积是解题的关键.

练习册系列答案
相关题目
 如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4
如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4| 2 |
A、
| ||
| B、3 | ||
| C、2 | ||
D、
|
抛物线y=-2(x-3)2+6的顶点坐标为( )
| A、(3,6) |
| B、(3,-6) |
| C、(-3,6) |
| D、(-3,-6) |
圆周上共有10个等分点,以其中三点为顶点的直角三角形的个数为( )
| A、20 | B、40 | C、60 | D、80 |