题目内容
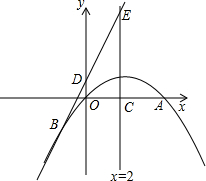 如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.
如图,已知二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2与x轴交于点C,直线y=2x+1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于D、E.(1)求这个二次函数的解析式;
(2)求证:D是BE的中点;
(3)若点P(x、y)是抛物线对称轴上的一个动点,是否存在这样的点P,使得△PBE是以PE为腰的等腰三角形?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把点B的坐标代入直线y=2x+1求出m的值,从而得到点B的坐标,再根据抛物线的对称性求出点A的坐标,然后利用待定系数法求二次函数解析式即可;
(2)令x=0,x=2求出点D、E的坐标,再根据两点之间的距离公式列式求出BD、DE的长度即可得证;
(3)因为腰不明确,所以分①PE=BE,根据BE的长度,分点P在点E的上方与下方两种情况写出,②PE=PB,设点P的坐标为(2,n)根据两点间的距离公式列式求出n的值为0,从而最后得解.
(2)令x=0,x=2求出点D、E的坐标,再根据两点之间的距离公式列式求出BD、DE的长度即可得证;
(3)因为腰不明确,所以分①PE=BE,根据BE的长度,分点P在点E的上方与下方两种情况写出,②PE=PB,设点P的坐标为(2,n)根据两点间的距离公式列式求出n的值为0,从而最后得解.
解答:(1)解:∵点B(-2,m)在直线y=2x+1上,
∴2×(-2)+1=m,
解得m=-3,
∴B(-2,-3),
∵二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2,
∴A(4,0),
∵二次函数y=ax2+bx+c的图象经过点O、A、B,
∴
,
解得
,
∴二次函数解析式为:y=-
x2+x;
(2)证明:∵直线y=2x+1与y轴、直线x=2分别交于D、E,
∴x=0时,y=1,
x=2时,y=2×2+1=5,
∴点D、E的坐标分别为:D(0,1)、E(2,5),
∴BD=
=2
,DE=
=2
,
∴BD=DE,
即D是BE的中点;
(3)解:抛物线的对称轴上存在这样的点P,使得△PBE是以PE为腰的等腰三角形.
①当PE=BE时,根据(2)的结论,PE=BD+DE=2
+2
=4
,
所以点P(2,5+4
)或 P(2,5-4
),
②当PE=PB时,设点P坐标为(2,n),
则PB=
=
,
PE=|n-5|,
所以
=|n-5|,
两边平方得,16+9+6n+n2=n2-10n+25,
解得n=0,
所以点P的坐标为P(2,0).
∴2×(-2)+1=m,
解得m=-3,
∴B(-2,-3),
∵二次函数y=ax2+bx+c的图象经过原点O和x轴上的另一点A,它的对称轴直线x=2,
∴A(4,0),
∵二次函数y=ax2+bx+c的图象经过点O、A、B,
∴
|
解得
|
∴二次函数解析式为:y=-
| 1 |
| 4 |
(2)证明:∵直线y=2x+1与y轴、直线x=2分别交于D、E,
∴x=0时,y=1,
x=2时,y=2×2+1=5,
∴点D、E的坐标分别为:D(0,1)、E(2,5),
∴BD=
| (-2)2+(-3-1)2 |
| 5 |
| 22+(5-1)2 |
| 5 |
∴BD=DE,
即D是BE的中点;
(3)解:抛物线的对称轴上存在这样的点P,使得△PBE是以PE为腰的等腰三角形.
①当PE=BE时,根据(2)的结论,PE=BD+DE=2
| 5 |
| 5 |
| 5 |
所以点P(2,5+4
| 5 |
| 5 |
②当PE=PB时,设点P坐标为(2,n),
则PB=
| (-2-2)2+(-3-n)2 |
| 16+(3+n)2 |
PE=|n-5|,
所以
| 16+(3+n)2 |
两边平方得,16+9+6n+n2=n2-10n+25,
解得n=0,
所以点P的坐标为P(2,0).
点评:本题是对二次函数的综合考查,有待定系数法求二次函数解析式,两点间的距离公式,以及等腰三角形的两腰相等,熟练运用两点间的距离公式是解题的关键.

练习册系列答案
相关题目
下列计算结果正确的是( )
| A、(-a3)2=a9 |
| B、a2•a3=a6 |
| C、a-2a=-a |
| D、a+a2=a3 |
 如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4
如图,有两个半径差1的圆,它们各有一个内接正八边形.已知阴影部分的面积是4| 2 |
A、
| ||
| B、3 | ||
| C、2 | ||
D、
|