题目内容
如图，直角梯形ABCD中，AD∥BC，∠A=90°，AD=1，BC=6，AB=5，P为AB上一点，若△PAD与△PBC相似，则AP=考点：相似三角形的性质
专题：
分析：设AP=x，表示出PB，然后根据相似三角形对应边成比例，分两种情况列出比例式，求解即可．
解答：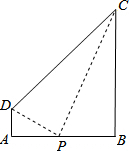
解：设AP=x，则PB=AB-AP=5-x，
∵△PAD与△PBC相似，
∴
=
，
即
=
，
解得x=
，
或
=
，
即
=
，
整理得，x2-5x+6=0，
解得x1=2，x2=3，
综上所述，AP的值为
或2或3．
故答案为：
或2或3．
解：设AP=x，则PB=AB-AP=5-x，∵△PAD与△PBC相似，
∴
| AP |
| AD |
| PB |
| BC |
即
| x |
| 1 |
| 5-x |
| 6 |
解得x=
| 5 |
| 7 |
或
| AP |
| AD |
| BC |
| PB |
即
| x |
| 1 |
| 6 |
| 5-x |
整理得，x2-5x+6=0，
解得x1=2，x2=3，
综上所述，AP的值为
| 5 |
| 7 |
故答案为：
| 5 |
| 7 |
点评：本题考查了相似三角形的性质，主要利用了相似三角形对应边成比例，难点在于分情况讨论．
练习册系列答案
导学教程高中新课标系列答案
相关题目
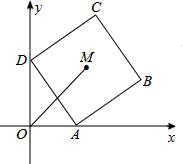在平面直角坐标系中，如图，点A的坐标是（2，0），点D在y轴的正半轴上，以线段AD为边向外作正方形ABCD如图所示，该正方形的中心M（3，3），那么点D的坐标为在△ABC中，已知∠A=3∠C=54°，则∠B的度数是（ ）
| A、90° | B、94° |
| C、98° | D、108° |
若x2-4x+a=（x-2）（x+b），则（ ）
| A、a=-4，b=2 |
| B、a=4，b=-2 |
| C、a=-4，b=-2 |
| D、a=4，b=2 |