题目内容
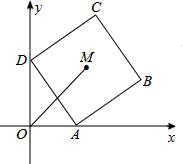 在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为
在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为考点:正方形的性质,待定系数法求一次函数解析式,全等三角形的判定与性质
专题:压轴题
分析:连接MA、MD,过点M作ME⊥x轴于E,作MF⊥y轴于F,根据点M的坐标判断出四边形OEMF是正方形,然后求出ME=MF,再利用“HL”证明Rt△AEM和Rt△DFM全等,根据全等三角形对应边相等可得DF=AE,再根据点A的坐标求出OA,然后求出AE,再求出OD,写出点D的坐标即可;
过点B作BG⊥x轴于G,求出∠ADO=∠BAG,然后利用“角角边”证明△AOD和△BAG全等,根据全等三角形对应边相等可得AG=OD,BG=OA,从而写出点B的坐标,过点C作CH⊥y轴于H,同理可得CH=OD,DH=OA,然后求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可.
过点B作BG⊥x轴于G,求出∠ADO=∠BAG,然后利用“角角边”证明△AOD和△BAG全等,根据全等三角形对应边相等可得AG=OD,BG=OA,从而写出点B的坐标,过点C作CH⊥y轴于H,同理可得CH=OD,DH=OA,然后求出点C的坐标,设直线BC的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式解答即可.
解答:解:如图,连接MA、MD,过点M作ME⊥x轴于E,作MF⊥y轴于F,
∵正方形ABCD的中心是M(3,3),
∴AM=DM,四边形OEMF是正方形,
∴ME=MF=3,
在Rt△AEM和Rt△DFM中,
,
∴Rt△AEM≌Rt△DFM(HL),
∴DF=AE,
∵A(2,0),
∴OA=2,
∴AE=OE-OA=3-2=1,
∴OD=OF+DF=OF+AE=3+1=4,
∴点D的坐标为(0,4);
过点B作BG⊥x轴于G,
∵∠ADO+∠OAD=90°,∠BAG+∠OAD=90°,
∴∠ADO=∠BAG,
在△AOD和△BAG中,
,
∴△AOD≌△BAG(AAS),
∴AG=OD=4,BG=OA=2,
∴OG=OA+AG=2+4=6,
∴点B的坐标为(6,2),
过点C作CH⊥y轴于H,
同理可得CH=OD=4,DH=OA=2,
∴OH=OD+DH=4+2=6,
∴点C的坐标为(4,6),
设直线BC的解析式为y=kx+b(k≠0),
则
,
解得
,
∴设直线BC的解析式为y=-2x+14.
故答案为:(0,4);y=-2x+14.
∵正方形ABCD的中心是M(3,3),
∴AM=DM,四边形OEMF是正方形,
∴ME=MF=3,
在Rt△AEM和Rt△DFM中,
|
∴Rt△AEM≌Rt△DFM(HL),
∴DF=AE,
∵A(2,0),

∴OA=2,
∴AE=OE-OA=3-2=1,
∴OD=OF+DF=OF+AE=3+1=4,
∴点D的坐标为(0,4);
过点B作BG⊥x轴于G,
∵∠ADO+∠OAD=90°,∠BAG+∠OAD=90°,
∴∠ADO=∠BAG,
在△AOD和△BAG中,
|
∴△AOD≌△BAG(AAS),
∴AG=OD=4,BG=OA=2,
∴OG=OA+AG=2+4=6,
∴点B的坐标为(6,2),
过点C作CH⊥y轴于H,
同理可得CH=OD=4,DH=OA=2,
∴OH=OD+DH=4+2=6,
∴点C的坐标为(4,6),
设直线BC的解析式为y=kx+b(k≠0),
则
|
解得
|
∴设直线BC的解析式为y=-2x+14.
故答案为:(0,4);y=-2x+14.
点评:本题考查了正方形的性质,全等三角形的判定与性质,待定系数法求一次函数解析式,难点在于作辅助线构造出全等三角形以及以点O、M为顶点的正方形.

练习册系列答案
相关题目
 如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化.
如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化. 如图,直角梯形ABCD中,AD∥BC,∠A=90°,AD=1,BC=6,AB=5,P为AB上一点,若△PAD与△PBC相似,则AP=
如图,直角梯形ABCD中,AD∥BC,∠A=90°,AD=1,BC=6,AB=5,P为AB上一点,若△PAD与△PBC相似,则AP= 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论: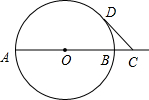 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.