题目内容
11.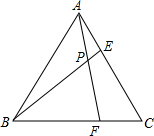 如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.
如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.(1)求∠APB的度数;
(2)若AE=2,求BP•BE的值.
分析 (1)证明△ABE≌△CAF,借用外角即可以得到答案;
(2)用平行线分线段成比例定理或者三角形相似定理即可以得到答案.
解答 (1)解:∵△ABC为等边三角形,
∴AB=AC,∠C=∠CAB=60°,
又∵AE=CF,
在△ABE和△CAF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠ACF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CAF(SAS),
∴AF=BE,∠ABE=∠CAF.
又∵∠APE=∠BPF=∠ABP+∠BAP,
∴∠APE=∠BAP+∠CAF=60°.
∴∠APB=180°-∠APE=120°.
(2)∵∠BAC=∠APE=60°,∠PAE=∠EBA,
∴△APE∽△ABE
∴$\frac{AE}{BE}=\frac{BP}{AB}$,
∴BP•BE=12
点评 本题考查了等边三角形性质的综合应用以及相似三角形的判定及性质的应用,解答本题的关键是注意转化思想的运用.

练习册系列答案
相关题目
2.三角形三边长分别为15、20、25,则最短边上的高为( )
| A. | 15 | B. | 20 | C. | 24 | D. | 25 |
1. 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 16$\sqrt{3}$ | B. | 24 | C. | 12$\sqrt{3}$ | D. | 12 |
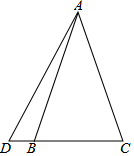 已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为2$\sqrt{10}$.
已知如图,△ABC为等腰三角形,D为CB延长线上一点,连AD且∠DAC=45°,BD=1,CB=4,则AC长为2$\sqrt{10}$.