题目内容
9.解下列不等式组:$\left\{\begin{array}{l}{x-1<3}\\{x+1<3}\end{array}\right.$.
分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式x-1<3,得:x<4,
解不等式x+1<3,得:x<2,
则不等式组的解集为x<2.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
14.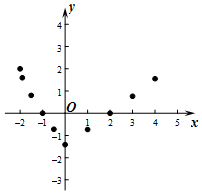 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.
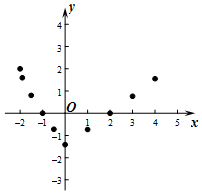 有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?
有这样一个问题:探究函数y=-$\sqrt{x+2}$+|x|的图象与性质.?小军根据学习函数的经验,对函数y=-$\sqrt{x+2}$+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=-$\sqrt{x+2}$+|x|的自变量x的取值范围是x≥-2;
(2)表是y与x的几组对应值?
| x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | … |
| y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | … |
(3)观察图象,函数的最小值是-$\sqrt{2}$;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外):当-2≤x<0时,y随x的增大而减小.
1. 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 16$\sqrt{3}$ | B. | 24 | C. | 12$\sqrt{3}$ | D. | 12 |
19. 如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
 如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )| A. | DG=$\frac{1}{2}$(a+b) | B. | CF=c-b | C. | BE=$\frac{1}{2}$(a-b) | D. | AE=$\frac{1}{2}$(b+c) |
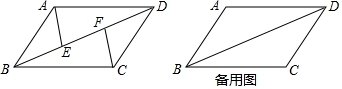
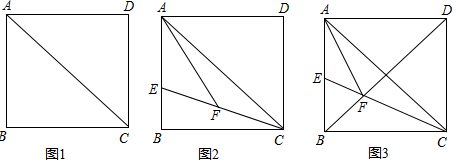

 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1.
如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为$\frac{9}{4}$或1.