��Ŀ����
3��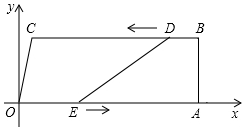 ��ͼ�����ı���OABC�У�OA��BC����OAB=90�㣬OΪԭ�㣬��C������Ϊ��2��8������A������Ϊ��26��0������D�ӵ�B��������ÿ��1����λ���ȵ��ٶ���BC���C�˶�����Eͬʱ�ӵ�O��������ÿ��3����λ���ȵ��ٶ�������OAB�˶�������E�ﵽ��Bʱ����DҲֹͣ�˶������˶���ʼ����D��E�����˶���ʱ��Ϊt�룮
��ͼ�����ı���OABC�У�OA��BC����OAB=90�㣬OΪԭ�㣬��C������Ϊ��2��8������A������Ϊ��26��0������D�ӵ�B��������ÿ��1����λ���ȵ��ٶ���BC���C�˶�����Eͬʱ�ӵ�O��������ÿ��3����λ���ȵ��ٶ�������OAB�˶�������E�ﵽ��Bʱ����DҲֹͣ�˶������˶���ʼ����D��E�����˶���ʱ��Ϊt�룮��1����tΪ��ֵʱ���ı���ABDE�Ǿ��Σ�
��2����tΪ��ֵʱ���ı���OEDC��ƽ���ı��Σ�
��3������AD���ǡ�ADE�����ΪS����S��t�ĺ�����ϵʽ��
���� ��1�����ݾ��ε��ж������г���ϵʽ�����㼴�ɣ�
��2������ƽ���ı��ε��ж����������ʶ������
��3���ֵ�E��OA�Ϻ͵�E��AB��������������������ε������ʽ���㼴��
��� �⣺��1���ߵ�C������Ϊ��2��8������A������Ϊ��26��0����
��OA=26��BC=24��AB=8��
��D��E�����˶���ʱ��Ϊt�룬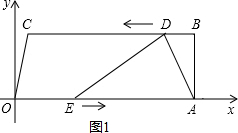
��BD=t��OE=3t��
���ı���ABDE�Ǿ��Σ�
��BD=AE��
��t=26-3t��
��ã�t=$\frac{13}{2}$��
��2�����ı���OEDCΪƽ���ı��Σ�
��CD=OE��
��24-t=3t��
��ã�t=6��
��3��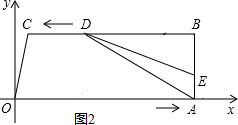 ��ͼ1������E��OA��ʱ��
��ͼ1������E��OA��ʱ��
AE=26-3t��
��S=$\frac{1}{2}$��AE��AB=$\frac{1}{2}$����26-3t����8=-12t+104��
����E��AB��ʱ��AE=3t-26��BD=t��
��S=$\frac{1}{2}$��AE��DB=$\frac{1}{2}$����3t-26����t=$\frac{1}{2}$t2-13t��
���� �������ı����ۺ��⣬��Ҫ�����˾��ε����ʣ�ƽ���ı��ε����ʣ������ε������ʽ��������ص����ʶ������ж�������������÷��������˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
13��һ������1��3��2��5��2��a��������a���������ݵ���λ���ǣ�������
| A�� | 3 | B�� | 2 | C�� | 1.5 | D�� | 2.5 |
12��ijУ�˶�Ա���з���ѵ������ÿ��5�ˣ���2�ˣ���ÿ��6�ˣ���ȱ3�ˣ����˶�Ա����Ϊx�ˣ�����Ϊy��������������з�����Ϊ��������
| A�� | $\left\{\begin{array}{l}{5y=x+2}\\{6x+3=x}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{5y=x+2}\\{6y-3=x}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x+3}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{5y=x-2}\\{6y=x-3}\end{array}\right.$ |
 ��ͼÿ��С�����εı߳���ʾ1���ף��밴Ҫ��ͼ�Σ�
��ͼÿ��С�����εı߳���ʾ1���ף��밴Ҫ��ͼ�Σ�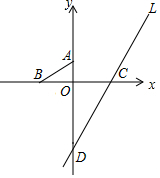 ��ͼ��������ƽ���ϣ�OΪԭ�㣬����A��0��3����B��-5��0����C��6��0�����㣬ֱ��Lͨ��C������y���ཻ��D�㣬��ش��������⣺
��ͼ��������ƽ���ϣ�OΪԭ�㣬����A��0��3����B��-5��0����C��6��0�����㣬ֱ��Lͨ��C������y���ཻ��D�㣬��ش��������⣺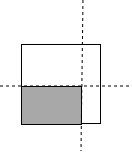 ijͬѧ����һ�����Ϊ400cm2��������ֽƬ������ͼ��ʾ�����űߵķ���ó�һ�����Ϊ300cm2�ij�����ֽƬ��ʹ���ij���֮��Ϊ3��2����������ѧ����֪ʶ��˵���ܷ������ֽƬ�ó�����Ҫ���ֽƬ��
ijͬѧ����һ�����Ϊ400cm2��������ֽƬ������ͼ��ʾ�����űߵķ���ó�һ�����Ϊ300cm2�ij�����ֽƬ��ʹ���ij���֮��Ϊ3��2����������ѧ����֪ʶ��˵���ܷ������ֽƬ�ó�����Ҫ���ֽƬ��