题目内容
8.解不等式组$\left\{\begin{array}{l}{4(x+1)+3>x①}\\{\frac{x-4}{2}≤\frac{x-5}{3}②}\end{array}\right.$,并把解集在数轴上表示出来,再求出符合条件的正整数解.分析 分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:解不等式①,得:x>-$\frac{7}{3}$,
解不等式②,得:x≤2,
∴不等式组的解集为-$\frac{7}{3}$<x≤2,
将解集表示在数轴上如下: ,
,
其正整数解为1.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 如图,?ABCD的对角线AC、BD相交于点O,若AB=5cm,BC=7cm,△COD的周长是17cm,则△BOC的周长是19cm.
如图,?ABCD的对角线AC、BD相交于点O,若AB=5cm,BC=7cm,△COD的周长是17cm,则△BOC的周长是19cm.
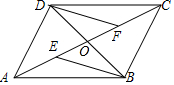 如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.
如图,四边形ABCD的对角线AC、BD相交于点O,且O是AC的中点,AE=CF,DF∥BE.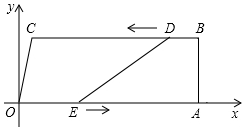 如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒. 如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.
如图,?ABCD中,G是CD的中点,E是边长AD上的动点,EG的延长线与BC的延长线相交于点F,连接CE,DF.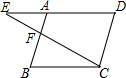 如图,点F在平行四边形ABCD的边AB上,且AF:BF=1:2,连接CF并延长,交DA的延长线于点E,若△AEF的面积为2,则平行四边形ABCD的面积为24.
如图,点F在平行四边形ABCD的边AB上,且AF:BF=1:2,连接CF并延长,交DA的延长线于点E,若△AEF的面积为2,则平行四边形ABCD的面积为24.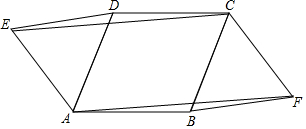 如图,以?ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形.
如图,以?ABCD的边AD、BC为边向外作等边三角形ADE和BCF,连接CE、AF,求证:四边形AECF是平行四边形.