题目内容
18.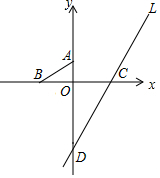 如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:
如图,在坐标平面上,O为原点,另有A(0,3),B(-5,0),C(6,0)三点,直线L通过C点且与y轴相交于D点,请回答下列问题:(1)已知直线L的方程为5x-3y=k,求k的值.
(2)承(1),请完整说明△AOB与△COD相似的理由.
分析 (1)利用函数图象上的点的特点,即可求出k的值;
(2)先求出OA,OB,OC,OD,即可得出$\frac{OA}{OC}=\frac{OB}{OD}$,即可得出结论.
解答 解:(1)∵直线L:5x-3y=k过点C(6,0),
∴5×6-3×0=k,
∴k=30,
(2)由(1)知,直线L:5x-3y=30,
∵直线L与y轴的交点为D,
令x=0,
∴-3y=30,
∴y=-10,
∴D(0,-10),
∴OD=10,
∵A(0,3),B(-5,0),C(6,0),
∴OA=3,OB=5,OC=6,
∴$\frac{OA}{OC}=\frac{3}{6}$=$\frac{1}{2}$,$\frac{OB}{OD}=\frac{5}{10}$=$\frac{1}{2}$,
∴$\frac{OA}{OC}=\frac{OB}{OD}$,
∵∠AOB=∠COD=90°,
∴△AOB∽△COD.
点评 此题是一次函数综合题,主要考查了函数图象上点的特点,相似三角形的判定,解本题的根据是求出点D的坐标.

练习册系列答案
相关题目
8.某公司销售一种进价为20元/个的水杯,其销售量y(万个)与销售价格x(元/个)的变化如下表,销售过程中的其他开支(不含成本)总计40万元.
(1)求出该公司销售这种水杯的净利润z(万元)与销售价格x(元/个)的函数关系式,并求出销售价格定为多少时净利润最大?最大值是多少?
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
7.把下面图形进行旋转可得到圆锥体的是( )
| A. |  | B. |  | C. |  |
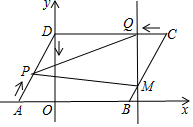 如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s.
如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s.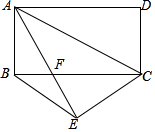 如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值.
如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值.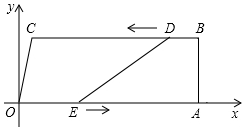 如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒. 如图,∠A=60°,O是AB上一点,直线OD与AB的夹角∠BOD为85°,要使OD∥AC,直线OD绕点O逆时针方向至少旋转25度.
如图,∠A=60°,O是AB上一点,直线OD与AB的夹角∠BOD为85°,要使OD∥AC,直线OD绕点O逆时针方向至少旋转25度.