题目内容
7. 如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )
如图,要测量河两岸相对的两点A、B的距离,先过点B作BF⊥AB,在BF上找点D,过D作DE⊥BF,再取BD的中点C,连接AC并延长,与DE交点为E,此时测得DE的长度就是AB的长度.这里判定△ABC和△EDC全等的依据是( )| A. | ASA | B. | SAS | C. | SSS | D. | AAS |
分析 根据条件可得到BC=CD,∠ABD=∠EDC,∠ACB=∠DCE,可得出所用的判定方法.
解答 解:
∵C为BD中点,
∴BC=CD,
∵AB⊥BF,DE⊥BF,
∴∠ABC=∠CDE=90°,且∠ACB=∠DCE,
∴在△ABC和△EDC中,满足ASA的判定方法,
故选A.
点评 本题主要考查三角形全等的判定方法,掌握全等三角形的五种判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
15.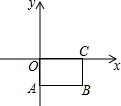 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
 已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )
已知,矩形OABC按如图所示的方式建立在平面直角坐标系总,AB=4,BC=2,则点B的坐标为( )| A. | (4,2) | B. | (-2,4) | C. | (4,-2) | D. | (-4,2) |
2.下列命题中:
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
12.反比例函数y=$\frac{1-5m}{x}$图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,y1<y2,则m的取值范围是( )
| A. | m>$\frac{1}{5}$ | B. | m<$\frac{1}{5}$ | C. | m≥$\frac{1}{5}$ | D. | m≤$\frac{1}{5}$ |
19.已知一次函数y=-x+b,过点(-8,-2),那么一次函数的解析式为( )
| A. | y=-x-2 | B. | y=-x-6 | C. | y=-x-10 | D. | y=-x-1 |
16. 如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
 如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )
如图,将一条两边沿互相平行的纸袋按如图所示折叠,已知∠1=40°,则∠α的度数( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
17.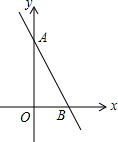 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
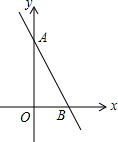 如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )
如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( )| A. | x>$\frac{3}{2}$ | B. | x>3 | C. | x<$\frac{3}{2}$ | D. | x<3 |
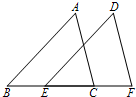 如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )
如图,△DEF是将△ABC沿射线BC的方向平移后得到的.若BC=5,EC=3,则CF的长为( )