题目内容
17.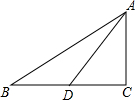 如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.
如图,在Rt△ABC中,∠ACB=90°,AD是边BC边上的中线,如果AD=BC,那么cot∠CAB的值是$\frac{\sqrt{3}}{2}$.
分析 设AD=BC=2x,利用中线定义得到CD=BD=x,则可根据勾股定理表示出AC,然后利用余切的定义求解.
解答 解:设AD=BC=2x,则CD=BD=x,
在Rt△ACD中,AC=$\sqrt{A{D}^{2}-C{D}^{2}}$=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
在Rt△ABC中,cot∠CAB=$\frac{AC}{BC}$=$\frac{\sqrt{3}x}{2x}$=$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活运用勾股定理和锐角三角函数的定义.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
8.若多项式a2+kab+b2是完全平方式,则常数k的值为( )
| A. | 2 | B. | 4 | C. | ±2 | D. | ±4 |
 如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.
如图,在△ABC上,点D、E分别是AC、BC边上的点,AE与BD交于点O,且CD=CE,∠1=∠2.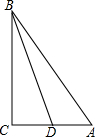 在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.
在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$. 如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论:
如图,AD、AE分别是△ABC的中线和角平分线,AC=2,AB=5,过点C作CF⊥AE于点F,连接DF,有下列结论: