题目内容
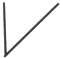
7.如图,在平面直角坐标系中,矩形OABC的三个顶点分别是A(3,0),B(3,4),C(0,4),点D在BC上,以D为顶点的抛物线经过点A,与x轴的另一个交点为E,且对称轴为x=1.(1)求抛物线的解析式;
(2)点P(m,0)是x轴的正半轴上的一个动点,过点P作DE的平行线,与折线C-B-A交于点Q,与抛物线交于点H,连接DE、AC、DE与OC、AC的交点分别为F,G.
①求△DGQ的面积S与m的函数关系式;
②当m为何值时,以点D、F、H、P为顶点的四边形为平行四边形.
分析 (1)由条件可先得出抛物线顶点坐标,从而直接将抛物线解析式设为顶点式,再将A点坐标代入即可求出解析式;
(2)①由△CDG∽△AEG算出DG,由于PQ∥DE,所以,过P作PM⊥DE于M,由△PEM∽FEO算出PM即可求出△DGQ的面积;
②分两种情况讨论:
当P在线段OA上,且PH∥DF,PH=DF时,四边形DFPH为平行四边形;
当P在线段OA的延长线上,且PH∥DF,PH=DF时,四边形DFPH为平行四边形.
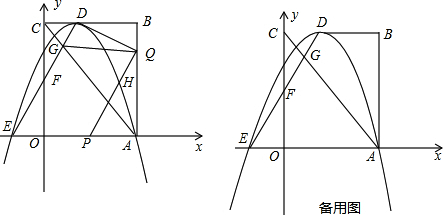
解答 解:(1)∵抛物线的顶点D的坐标为(1,4),
∴设抛物线的解析式为y=a(x-1)2+4,
把点A的坐标为(3,0)代入抛物线的解析式得:4a+4=0
解得a=-1.
∴抛物线的解析式为y=-(x-1)2+4,即y=-x2+2x+3.
(2)①当y=0时,-x2+2x+3=0.
解得x1=-1,x2=3,
∴E点坐标为(-1,0),AE=4.
∴OE=CD=1,
∴△EOF≌△DCF.
∴OF=CF=$\frac{1}{2}$,OC=2.
根据勾股定理,EF=DF=2$\sqrt{5}$,
∴DE=4$\sqrt{5}$.
∵CD∥AE,∴△CDG∽△AEG,∴$\frac{DG}{GE}=\frac{CD}{AE}=\frac{1}{4}$.
∴DG=$\frac{1}{5}$,DE=$\frac{2\sqrt{5}}{5}$.
过点P作PM⊥DE,垂足为M,如图,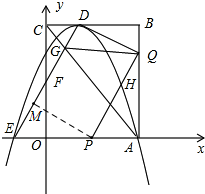
则△PEM∽FEO,得$\frac{PM}{PE}=\frac{OF}{EF}$,
∴$\frac{PM}{m+1}=\frac{2}{\sqrt{5}}$,
∴PM=$\frac{2\sqrt{5}}{5}(m+1)$,
∴△DGQ的面积S与m的函数关系式为:
S=$\frac{1}{2}$DG•PM=$\frac{1}{2}$×$\frac{2\sqrt{5}}{5}$×$\frac{2\sqrt{5}}{5}$(m+1),即S=$\frac{2}{5}m+\frac{2}{5}$(0≤m≤3).
②分两种情况:
如图,当P在线段OA上,且PH∥DF,PH=DF时,四边形DFPH为平行四边形,
过H作HN⊥OA,垂足为N,这时易证△CDF≌△NPH,
∴PN=CD=1,HN=CF=2,
∴H点的坐标为(m+1,2)把H点的坐标代入抛物线的解析式得:
-(m+1)2+2(m+1)+3=2
解得m=$\sqrt{2}$或m=-$\sqrt{2}$(不合题意,舍去)
如图,当P在线段OA的延长线上,且PH∥DF,PH=DF时,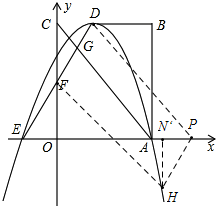
四边形DFHP为平行四边形,
过H作HN′⊥OA,垂足为N′,同理可得△CDF≌N′PH,
∴PN′=CD=1,HN′=CF=2,
∴H点的坐标为(m-1,-2)
把H点的坐标代入抛物线的解析式得:
-(m-1)2+2(m-1)+3=-2,
解得m=2+$\sqrt{6}$或m=2-$\sqrt{6}$(不合题意,舍去)
∴当m的值为$\sqrt{2}$或2+$\sqrt{6}$时,以点D,F,H,P为顶点的四边形为平行四边形.
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数解析式、全等三角形的判定与性质、相似三角形的判定与性质、三角形面积求法、平行四边形的判定与性质、一元二次方程的解法等知识点,难度中等.注意最后一问分类讨论思想的应用.

| A. | 0 | B. | 1 | C. | -1 | D. | ±1 |
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
| A. | 了解江苏教育节目“服务到家”栏目的收视率 | |
| B. | 了解某甲型H1N1确诊病人同机乘客的健康状况 | |
| C. | 了解某班每个学生家庭电脑的数量 | |
| D. | 企业在给职工做工作服前进行的尺寸大小的调查 |
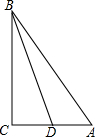 在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.
在Rt△ACB中,∠C=90°,点D是AC的中点,cos∠CBD=$\frac{{\sqrt{15}}}{4}$,则sin∠ABD=$\frac{\sqrt{285}}{76}$.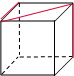 一个全透明的正方体上面放有一根黑色的金属丝(如图),那么金属丝在左视图中的形状是( )
一个全透明的正方体上面放有一根黑色的金属丝(如图),那么金属丝在左视图中的形状是( )