题目内容
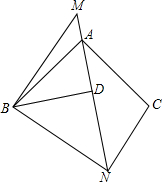如图，已知△ABC和△MBN都是等腰直角三角形，∠BAC=∠MBN=90°，BD⊥AN．请找出与△ABD相似的三角形并给出证明，直接写出∠ANC的度数．考点：相似三角形的判定
专题：
分析：利用两边对应比值相等且夹角相等的两三角形相似，进而求出即可．
解答：
解：△ABD∽△CBN，
理由：∵△ABC和△MBN都是等腰直角三角形，BD⊥AN，
∴∠MBD=∠NBD=∠BNM=∠ABC=45°，
∴
=
=
，
∵∠MBA+∠ABD=45°，∠ABD+∠CBN=45°，
∴∠ABD=∠CBN，
∴△ABD∽△CBN，
∴∠BNC=∠ADB=90°，
∵∠BNA=45°，
∴∠ANC=45°．
解：△ABD∽△CBN，理由：∵△ABC和△MBN都是等腰直角三角形，BD⊥AN，
∴∠MBD=∠NBD=∠BNM=∠ABC=45°，
∴
| BD |
| BN |
| AB |
| BC |
| ||
| 2 |
∵∠MBA+∠ABD=45°，∠ABD+∠CBN=45°，
∴∠ABD=∠CBN，
∴△ABD∽△CBN，
∴∠BNC=∠ADB=90°，
∵∠BNA=45°，
∴∠ANC=45°．
点评：此题主要考查了相似三角形的判定，得出
=
是解题关键．
| BD |
| BN |
| AB |
| BC |
练习册系列答案
相关题目
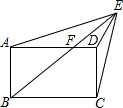如图，在长方形ABCD的外侧取点E，将各顶点用直线连接，AD和EB的交点是F．当△EAF的面积是18平方厘米；四边形FBCD的面积是50平方厘米；△EDC的面积是8平方厘米时，求△EFD的面积．
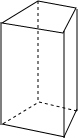观察如图所示的直四棱柱．
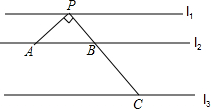如图，直线l1∥l2∥l3，l1与l2之间的距离为1，l2与l3之间的距离为2，点P在l1上，点A在l2上，点C在l3上，PC交l2于点B，PA⊥PC．
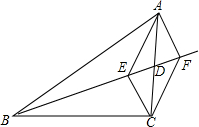如图，BD是△ABC的中线，CE⊥BD于点E，AF⊥BD交BD的延长线于点F．
直线y=2x+3与直线y=-2x-1的图象如图所示．