题目内容
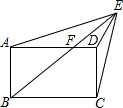 如图,在长方形ABCD的外侧取点E,将各顶点用直线连接,AD和EB的交点是F.当△EAF的面积是18平方厘米;四边形FBCD的面积是50平方厘米;△EDC的面积是8平方厘米时,求△EFD的面积.
如图,在长方形ABCD的外侧取点E,将各顶点用直线连接,AD和EB的交点是F.当△EAF的面积是18平方厘米;四边形FBCD的面积是50平方厘米;△EDC的面积是8平方厘米时,求△EFD的面积.考点:面积及等积变换
专题:
分析:过E作EG⊥AD交AD的延长线与G,连接BD,由三角形EFD的面积等于三角形EBC的面积减去三角形EDC的面积再减去四边形FBCD的面积及S△EBC=
BC(EG+DC)得出平行四边形ABCD的面积,又可得到△ABF及△BFD的面积,从而得出AF:FD的值,再结合△AEF的面积可求得△EFD的面积.
| 1 |
| 2 |
解答:解:如图,过E作EG⊥AD交AD的延长线与G,连接BD

∵S△EFD=S△EBC-S△EDC-S四边形FBCD,
∵S△EBC=
BC(EG+DC)=
BC×EG+
BC×CD
=S△AED+
S四边形ABCD,
=S△AFE+S△EFD+
S四边形ABCD;
=18+S△EFD+
S四边形ABCD;
∴S△EFD=18+S△EFD+
S四边形ABCD-58;
∴
S四边形ABCD=40(平方厘米),
∴S四边形ABCD=40×2=80(平方厘米),
又∵四边形FBCD的面积是50平方厘米,
∴s△ABF=80-50=30(平方厘米),
∴S△BFD=10平方厘米,
∴AF:FD=3:1,
∴S△EFD=
×S△AEF=
×18=6(平方厘米)
答:三角形EFD的面积是6平方厘米.

∵S△EFD=S△EBC-S△EDC-S四边形FBCD,
∵S△EBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=S△AED+
| 1 |
| 2 |
=S△AFE+S△EFD+
| 1 |
| 2 |
=18+S△EFD+
| 1 |
| 2 |
∴S△EFD=18+S△EFD+
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴S四边形ABCD=40×2=80(平方厘米),
又∵四边形FBCD的面积是50平方厘米,
∴s△ABF=80-50=30(平方厘米),
∴S△BFD=10平方厘米,
∴AF:FD=3:1,
∴S△EFD=
| 1 |
| 3 |
| 1 |
| 3 |
答:三角形EFD的面积是6平方厘米.
点评:本题主要考查了面积及等积变换,恰当添加辅助线,求出四边形ABCD的面积是解答此题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
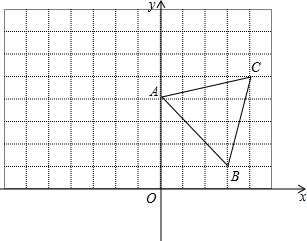 已知在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,1),点C的坐标为(4,5),将△ABC绕原点O逆时针旋转90°,得到△A1B1C1,(其中点A转到点A1处,点B转到点B处).
已知在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(3,1),点C的坐标为(4,5),将△ABC绕原点O逆时针旋转90°,得到△A1B1C1,(其中点A转到点A1处,点B转到点B处).
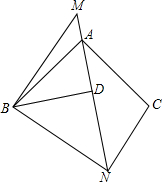 如图,已知△ABC和△MBN都是等腰直角三角形,∠BAC=∠MBN=90°,BD⊥AN.请找出与△ABD相似的三角形并给出证明,直接写出∠ANC的度数.
如图,已知△ABC和△MBN都是等腰直角三角形,∠BAC=∠MBN=90°,BD⊥AN.请找出与△ABD相似的三角形并给出证明,直接写出∠ANC的度数.