题目内容
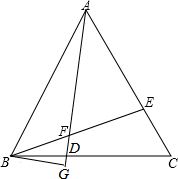 已知△ABC是等边三角形,BD=CE,BG⊥AD于G,求证:
已知△ABC是等边三角形,BD=CE,BG⊥AD于G,求证:(1)∠BFD=60°;
(2)BF=2FG.
考点:全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形
专题:证明题
分析:(1)由条件可证明△ABD≌△BCE,得到∠FBD=∠BAD,再利用外角性质可得∠BFD=∠FBA+∠BAF=∠FBA+∠FBD=∠ABC=60°;
(2)在Rt△BGF中,由30°角所对的直角边是斜边的一半可得出结论.
(2)在Rt△BGF中,由30°角所对的直角边是斜边的一半可得出结论.
解答:证明:(1)∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠FBD=∠BAF,
∵∠BFD=∠FBA+∠BAF,
∴∠BFD=∠FBA+∠FBD=∠ABC=60°;
(2)在Rt△BGF中,∠BFD=60°,
∴∠FBG=30°,
∴BF=2FG.
∴AB=BC,∠ABC=∠C=60°,
在△ABD和△BCE中,
|
∴△ABD≌△BCE(SAS),
∴∠FBD=∠BAF,
∵∠BFD=∠FBA+∠BAF,
∴∠BFD=∠FBA+∠FBD=∠ABC=60°;
(2)在Rt△BGF中,∠BFD=60°,
∴∠FBG=30°,
∴BF=2FG.
点评:本题主要考查等边三角形的性质及全等三角形的判定和性质的应用,由条件证明△ABD≌△BCE是解题的关键.

练习册系列答案
相关题目
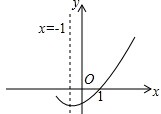 已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )
已知二次函数y=ax2+bx+c图象一部分,下面判断正确的有( )| A、a+b+c=0 |
| B、b>2a |
| C、ax2+bx+c=0两根是-3和1 |
| D、a-2b+c>0 |
下面是按一定规律排列的一列数:
第1个数:
-(1+
);
第2个数:
-(1+
)(1+
)(1+
);
第3个数:
-(1+
)(1+
)(1+
)(1+
)(1+
);
…
第n个数:
-(1+
)(1+
)(1+
)…(1+
).
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
第1个数:
| 1 |
| 2 |
| -1 |
| 2 |
第2个数:
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数:
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
第n个数:
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
| A、第2011个数 |
| B、第2012个数 |
| C、第2013个数 |
| D、第2014个数 |
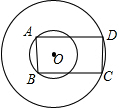 如图所示:两个同心圆,半径分别是2
如图所示:两个同心圆,半径分别是2| 6 |
| 3 |
A、22+6
| ||
B、20+8
| ||
C、18+10
| ||
D、16+12
|
下列各式中结果为负数的是( )
| A、-(-3) |
| B、(-3)2 |
| C、|-3| |
| D、-|-3| |
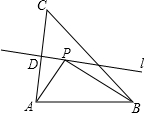 如图,AC的垂直平分线l交AC于点D,BC=4,点P在直线l上,则PB+PA的最小值是
如图,AC的垂直平分线l交AC于点D,BC=4,点P在直线l上,则PB+PA的最小值是 已知:△ABC
已知:△ABC