题目内容
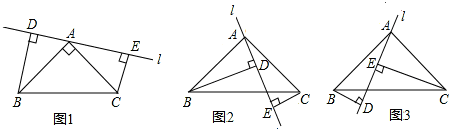
在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:BD=DE+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD-CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
(1)当直线l绕点A旋转到如图1位置时,试说明:BD=DE+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD-CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.

考点:全等三角形的判定与性质
专题:
分析:(1)利用条件证明△ABD≌△CAE,再结合线段的和差可得出结论;
(2)同(1)可证明△ABD≌△CAE,再结合线段的和差可得出结论;
(3)同理可证明△ABD≌△CAE,再结合线段的和差可得出结论.
(2)同(1)可证明△ABD≌△CAE,再结合线段的和差可得出结论;
(3)同理可证明△ABD≌△CAE,再结合线段的和差可得出结论.
解答:(1)证明:如图1,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AE-AD,
∴DE=BD-CE.
(3)DE=CE-BD
如图3,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AD-AE,
∴DE=CE-BD.
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AE-AD,
∴DE=BD-CE.
(3)DE=CE-BD
如图3,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
|
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AD-AE,
∴DE=CE-BD.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定是解题的关键,判定三角形全等的方法有SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
下面是按一定规律排列的一列数:
第1个数:
-(1+
);
第2个数:
-(1+
)(1+
)(1+
);
第3个数:
-(1+
)(1+
)(1+
)(1+
)(1+
);
…
第n个数:
-(1+
)(1+
)(1+
)…(1+
).
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
第1个数:
| 1 |
| 2 |
| -1 |
| 2 |
第2个数:
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数:
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
第n个数:
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
那么,在第2011个数、第2012个数、第2013个数、第2014个数中,最大的数是( )
| A、第2011个数 |
| B、第2012个数 |
| C、第2013个数 |
| D、第2014个数 |
 已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).
已知AB是⊙O的一条弦,在圆上作出点C,使得△ABC为等腰三角形(请在图中作出满足条件的所有点C,不写作法,保留作图痕迹).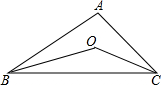 如图,O是△ABC的内心,∠BOC=100°,则∠A=
如图,O是△ABC的内心,∠BOC=100°,则∠A= △ABC中,∠C=90°,⊙O是△ABC的内切圆.AB=8,⊙O的半径为2,则△ABC的周长是
△ABC中,∠C=90°,⊙O是△ABC的内切圆.AB=8,⊙O的半径为2,则△ABC的周长是 已知AB⊥BF,DE⊥BF,垂足分别为点B、E,C为BF上的一点,且AB=DE,AC=DF,求证:BE=CF.
已知AB⊥BF,DE⊥BF,垂足分别为点B、E,C为BF上的一点,且AB=DE,AC=DF,求证:BE=CF.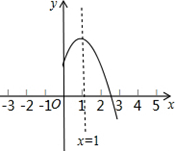 二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0.其中判断正确的有( )个.
二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,其图象的一部分如图所示则①abc<0;②a-b+c<0;③3a+c<0;④当-1<x<3时,y>0.其中判断正确的有( )个.