题目内容
计算：（
a3-0.9ax3）÷
ax3．
| 6 |
| 5 |
| 3 |
| 5 |
考点：整式的除法
专题：
分析：利用乘法分配律求解即可．
解答：解：（
a3-0.9ax3）÷
ax3
=
a3×
-
ax3×
，
=
-
．
| 6 |
| 5 |
| 3 |
| 5 |
=
| 6 |
| 5 |
| 5 |
| 3ax3 |
| 9 |
| 10 |
| 5 |
| 3ax3 |
=
| 2a2 |
| x3 |
| 3 |
| 2 |
点评：本题主要考查了整式的除法，解题的关键是利用乘法分配律求解．
练习册系列答案
阅读快车系列答案
相关题目
下面是按一定规律排列的一列数：
第1个数：
-（1+
）；
第2个数：
-（1+
）（1+
）（1+
）；
第3个数：
-（1+
）（1+
）（1+
）（1+
）（1+
）；
…
第n个数：
-（1+
）（1+
）（1+
）…（1+
）．
那么，在第2011个数、第2012个数、第2013个数、第2014个数中，最大的数是（ ）
第1个数：
| 1 |
| 2 |
| -1 |
| 2 |
第2个数：
| 1 |
| 3 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
第3个数：
| 1 |
| 4 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)4 |
| 5 |
| (-1)5 |
| 6 |
…
第n个数：
| 1 |
| n+1 |
| -1 |
| 2 |
| (-1)2 |
| 3 |
| (-1)3 |
| 4 |
| (-1)2n-1 |
| 2n |
那么，在第2011个数、第2012个数、第2013个数、第2014个数中，最大的数是（ ）
| A、第2011个数 |
| B、第2012个数 |
| C、第2013个数 |
| D、第2014个数 |
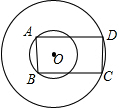如图所示：两个同心圆，半径分别是2| 6 |
| 3 |
A、22+6
| ||
B、20+8
| ||
C、18+10
| ||
D、16+12
|
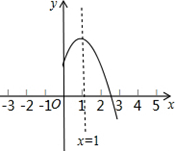二次函数y=ax2+bx+c（a≠0）的图象的对称轴是直线x=1，其图象的一部分如图所示则①abc＜0；②a-b+c＜0；③3a+c＜0；④当-1＜x＜3时，y＞0．其中判断正确的有（ ）个．| A、1 | B、2 | C、3 | D、4 |
在数轴上表示数a的点到原点的距离是3个单位长度，则-a+|a|的值为（ ）
| A、0 | B、3 | C、0或6 | D、0或-6 |