题目内容
20．已知直线AB、CD相交于点O，且A、B和C、D分别位于点O两侧，OE⊥AB，∠DOE=40°，则∠AOC=50°或130°．分析 分成A和E在CD的同一侧和当A和E在CD的两侧时两种情况进行讨论，利用角的和差即可求解．
解答 解：当A和E在CD的同一侧时，如图1．
∵OE⊥AB，
∴∠AOE=90°，
∴∠AOC=180°-∠AOE-∠DOE=180°-90°-40°=50°；
当A和E在CD的两侧时，如图2．
∠AOD=90°-∠EOD=90°-40°=50°，
则∠AOC=180°-∠AOD=180°-50°=130°．
故答案是：50°或130°．
点评 本题考查了角度的计算，角度的计算一般转化为角度的和或差计算，注意两种情况讨论是关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
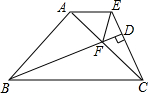如图，△ABC中，∠BAC=90°，AB=AC，AE∥BC，BD⊥CE于点D，BD交AC于F，连结EF．求证：BF=CE+EF．
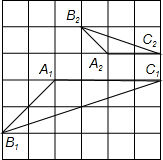学习相似三角形和解直角三角形的相关内容后，张老师请同学们交流这样的一个问题：“如图，在正方形网格上有△A1B1C1和△A2B2C2，这两个三角形是否相似？”．那么你认为△A1B1C1和△A2B2C2相似．（填相似或不相似）；理由是$\frac{{A}_{1}{B}_{1}}{{A}_{2}{B}_{2}}$=$\frac{{B}_{1}{C}_{1}}{{B}_{2}{C}_{2}}$=$\frac{{A}_{1}{C}_{1}}{{A}_{2}{C}_{2}}$．
12．在△ABC中，∠C=90°，BC=3，AB=5，则sinA的值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{3}{4}$ |
如图，小明从路灯下A处，向前走了5米到达D处，行走过程中，他的影子将会（只填序号）①．①越来越长，②越来越短，③长度不变．