题目内容
13.若|a-b+2|与$\sqrt{a-1}$互为相反数,求21a+2b的立方根.分析 根据互为相反数的两个数的和等于0列式,再根据非负数的性质列式求出a、b的值,然后代入代数式求出其值,再根据立方根的定义解答.
解答 解:∵|a-b+2|与$\sqrt{a-1}$互为相反数,
∴|a-b+2|+$\sqrt{a-1}$=0,
∴$\left\{\begin{array}{l}{a-b+2=0\\;}\\{a-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$,
∴21a+2b=21×1+2×3=27,
∵33=27,
∴21a+2b的立方根是3.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0;解二元一次方程组,以及代数式求值和立方根的定义,是基础题,列出方程求出a、b的值是解题的关键.

练习册系列答案
相关题目
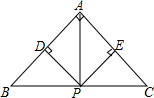 在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:
在△ABC,点P是BC边的中点,PD⊥AB于点D,PE⊥AC于点E,求证:

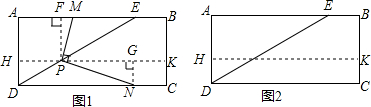
 如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米.
如图,矩形ABCD为某中学课外活动小组围建的一个生物苗圃园,其中两边靠墙(墙足够长),另外两边用长度为16米的篱笆(虚线部分)围成.设AB边的长度为x米,矩形ABCD的面积为y平方米. 作图题
作图题