Question

9．如图1，梯形ABCD中，AD∥BC，AB=AD=DC=5，BC=11．一个动点P从点B出发，以每秒1个单位长度的速度沿线段BC方向运动，过点P作PQ⊥BC，交折线段BA-AD于点Q，以PQ为边向右作正方形PQMN，点N在射线BC上，当Q点到达D点时，运动结束．设点P的运动时间为t秒（t＞0）．
（1）当正方形PQMN的边MN恰好经过点D时，求运动时间t的值；
（2）如图2，当点Q在线段AD上运动时，线段PQ与对角线BD交于点E，将△DEQ沿BD翻折，得到△DEF，连接PF．是否存在这样的t，使△PEF是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．

Answer 1

分析 （1）作AG⊥BC，DH⊥BC，垂足分别为G、H，可以得出四边形AGHD为矩形，根据矩形的性质及相关条件可以得出△ABG≌△DCH，可以求出BG=CH的值，再由勾股定理就可以求出AG=DH的值，就可以求出BP的值，即可以求出结论t的值；
（2）先由条件可以求出EF=EQ=PQ-EP=4-$\frac{1}{2}$t，分为三种情况：EF=EP时可以求出t值；当FE=FP时，作FR⊥EP，垂足为R，可以求出t值；当PE=PF时，作PS⊥EF，垂足为S，可以求出t值；即可得出结果．

解答 解：（1）如图2，作AG⊥BC，DH⊥BC，垂足分别为G、H，
∴四边形AGHD为矩形．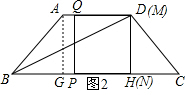
∵梯形ABCD，AB=AD=DC=5，
∴△ABG≌△DCH，
∴BG=$\frac{1}{2}$（BC-AD）=3，AG=4，
∴当正方形PQMN的边MN恰好经过点D时，点M与点D重合，此时MQ=4，
∴GP=AQ=AD-DQ=1，BP=BG+GP=4，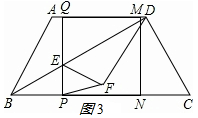
∴t=4，
即4秒时，正方形PQMN的边MN恰好经过点D；
（2）∵∠PEF+∠QEF=180°=∠QDF+∠QEF，
∴∠PEF=∠QDF=2∠ADB=∠ABC，
∴cos∠ABC=cos∠PEF=$\frac{3}{5}$，
由（1）可知EP=$\frac{1}{2}$BP=$\frac{1}{2}$t，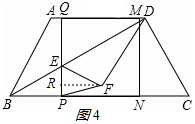
则EF=EQ=PQ-EP=4-$\frac{1}{2}$t，
①如图3，当EF=EP时，4-$\frac{1}{2}$t=$\frac{1}{2}$t，
∴t=4；
②如图4，当FE=FP时，作FR⊥EP，垂足为R，
∴ER=$\frac{1}{2}$EP=$\frac{3}{5}$EF，
∴$\frac{1}{2}$×$\frac{1}{2}$t=$\frac{3}{5}$（4-$\frac{1}{2}$t），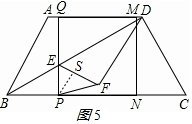
∴t=$\frac{48}{11}$；
③如图5，当PE=PF时，作PS⊥EF，垂足为S，
∵ES=$\frac{1}{2}$EF=$\frac{3}{5}$PE，
∴$\frac{1}{2}$（4-$\frac{1}{2}$t）=$\frac{3}{5}$×$\frac{1}{2}$t，
∴t=$\frac{40}{11}$．
∴当t=4或$\frac{48}{11}$或$\frac{40}{11}$时，△PEF是等腰三角形．

点评 本题是四边形综合题目，考查了动点问题的运用，等腰直角梯形的性质的运用，全等三角形的判定及性质，等腰三角形的性质等知识；本题综合性强，有一定难度，特别是（2）中需要进行分类讨论才能得出结果．