题目内容
7．
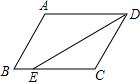如图，在?ABCD中，AD=8cm，AB=6cm，DE平分∠ADC，交BC边于点E，则BE的长为（ ）| A． | 2cm | B． | 4cm | C． | 6cm | D． | 8cm |
分析 由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA=∠DEC，而DE平分∠ADC，进一步推出∠EDC=∠DEC，根据等角对等边得CE=CD，则BE可求解．
解答 解：根据平行四边形的性质得AD∥BC，
∴∠EDA=∠DEC，
又∵DE平分∠ADC，
∴∠EDC=∠ADE，
∴∠EDC=∠DEC，
∴CD=CE=AB=6，
∴BE=BC-EC=8-6=2（cm）．
故选：A．
点评 本题考查了平行四边形性质、等腰三角形的判定；熟练掌握平行四边形的性质，证明CE=CD是解决问题的关键．
练习册系列答案
相关题目
17．已知正方形的边长为a，面积为S，则（ ）
| A． | a=$\sqrt{S}$ | B． | a=$\sqrt{S}$ | C． | S=$\sqrt{a}$ | D． | S=±$\sqrt{a}$ |
18．
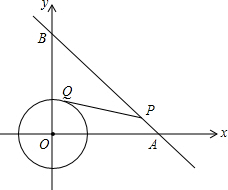如图，⊙O是以原点为圆心，$\sqrt{2}$为半径的圆，点P是直线y=-x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则S△PQO的最小值为（ ）
如图，⊙O是以原点为圆心，$\sqrt{2}$为半径的圆，点P是直线y=-x+6上的一点，过点P作⊙O的一条切线PQ，Q为切点，则S△PQO的最小值为（ ）| A． | 3 | B． | 4$\sqrt{2}$ | C． | 6-$\sqrt{2}$ | D． | 2$\sqrt{2}$ |
如图，已知∠1=∠2，BD平分∠ABC，可得到那两条直线平行？如果要得到另外两条直线平行，则应将上述两个条件之一做如何改变？
如图，⊙O的直径AB=4，AC是弦，沿AC折叠劣弧$\widehat{AB}$，记折叠后的劣弧为$\widehat{AmC}$，当$\widehat{AmC}$经过圆心O时，图中阴影部分的面积为$\sqrt{3}$；当$\widehat{AmC}$与直径AB交于点D时，设AC=x，BD=y，则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8．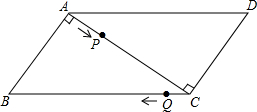
已知，如图，用两块一样大的直角三角板拼成一个平行四边形，∠BAC=∠ACD=90°．在?ABCD中，AB=3cm，BC=5cm，点P自A向C、沿AC的方向匀速运动，速度为1cm/s；同时，点Q从点C出发，自C向B、沿CB方向匀速运动，速度为1cm/s；过点P作PM⊥AD，并与AD相交于点M，当P、Q中有一个点到达终点时，另一个点也停止运动．设运动时间为t（s）．解答下列问题：