题目内容
13.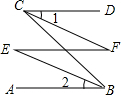 如图,已知AB∥CD,试再添上一个条件,就可证明∠1=∠2,试用两种方法证明.
如图,已知AB∥CD,试再添上一个条件,就可证明∠1=∠2,试用两种方法证明.
分析 可以添加CF∥BE,或添加∠E=∠F,证得CF∥BE,然后由两直线平行,内错角相等,证得结论.
解答 解:法一:添:CF∥BE,
证明:∵AB∥CD,CF∥BE,
∴∠DCB=∠ABC,∠FCB=∠EBC,
∴∠DCB-∠FCB=∠ABC-∠EBC,
∴∠1=∠2;
法二:添:∠E=∠F.
证明:∵∠E=∠F,
∴CF∥BE,
∴∠FCB=∠EBC,
∵AB∥CD,
∴∠DCB=∠ABC,
∴∠DCB-∠FCB=∠ABC-∠EBC,
∴∠1=∠2.
点评 此题考查了平行线的性质与判定.注意掌握两直线平行,内错角相等定理的应用是解此题的关键.

练习册系列答案
相关题目
18.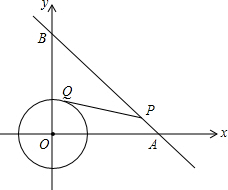 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则S△PQO的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 6-$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
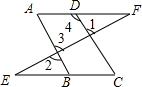 如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC.
如图,已知∠1=∠2,∠A=∠C,证明:AF∥EC. 如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧$\widehat{AB}$,记折叠后的劣弧为$\widehat{AmC}$,当$\widehat{AmC}$经过圆心O时,图中阴影部分的面积为$\sqrt{3}$;当$\widehat{AmC}$与直径AB交于点D时,设AC=x,BD=y,则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8.
如图,⊙O的直径AB=4,AC是弦,沿AC折叠劣弧$\widehat{AB}$,记折叠后的劣弧为$\widehat{AmC}$,当$\widehat{AmC}$经过圆心O时,图中阴影部分的面积为$\sqrt{3}$;当$\widehat{AmC}$与直径AB交于点D时,设AC=x,BD=y,则y关于x的函数关系式为y=-$\frac{1}{2}$x2+8.