题目内容
13. 如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 根据图象直接写出kx+b-$\frac{6}{x}$<0的x的取值范围:0<x<1或x>3.
如图,一次函数y=kx+b与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(m,6),B(3,n)两点. 根据图象直接写出kx+b-$\frac{6}{x}$<0的x的取值范围:0<x<1或x>3.
分析 先把A、B的坐标代入反比例函数的解析式,求出A、B的坐标,根据两点的坐标和图象得出即可.
解答 解:把A、B的坐标代入反比例函数y=$\frac{6}{x}$得:m=1,n=2,
即A的坐标为(1,6),B的坐标为(3,2),
所以kx+b-$\frac{6}{x}$<0的x的取值范围为0<x<1或x>3,
故答案为:0<x<1或x>3.
点评 本题考查的是正比例函数与反比例函数的交点问题,能根据图象和两个点的坐标得出答案是解此题的关键,注意:数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.下列关系中,互相垂直的两条直线是( )
| A. | 互为对顶角的两角的平分线 | |
| B. | 两直线相交成的四角中相邻两角的角平分线 | |
| C. | 互为补角的两角的平分线 | |
| D. | 相邻两角的角平分线 |
1.盒子中装有2个红球和4个绿球,每个球除颜色外完全相同,从盒子中任意摸出一个球,是绿球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
18.不等式组$\left\{\begin{array}{l}x-3>2\\ x<3\end{array}\right.$的解集是( )
| A. | x<3 | B. | 3<x<5 | C. | x>5 | D. | 无解 |
2. 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=5cm,AD⊥BC于D,则BD=( )| A. | 10cm | B. | 7.5cm | C. | 8.5cm | D. | 6.5cm |
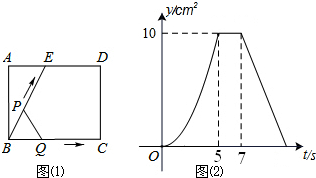 如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似.
如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图(2),当t=$\frac{29}{4}$秒时,△ABE与△BQP相似. 已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
已知,如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.