题目内容
2．
如图，已知菱形ABCD中，AC，BD相交于点O，点E是AB的中点，OE=5cm，则菱形的周长是40cm．
分析 由菱形ABCD中，AC，BD相交于点O，点E是AB的中点，OE=5cm，利用三角形中位线的性质，可求得BC的长，然后由菱形的性质，求得答案．
解答 解：∵菱形ABCD中，AC，BD相交于点O，
∴OA=OC，
∵点E是AB的中点，OE=5cm，
∴BC=2OE=10cm，
∴菱形的周长是：4BC=40cm．
故答案为：40．
点评 此题考查了菱形的性质以及三角形中位线的性质．注意掌握菱形的对角线互相平分、四条边都相等定理的应用是解此题的关键．
练习册系列答案
相关题目
10．
如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=$\sqrt{6}$，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD+CE=（ ）
如图，在等腰直角△ABC中，∠C=90°，点O是AB的中点，且AB=$\sqrt{6}$，将一块直角三角板的直角顶点放在点O处，始终保持该直角三角板的两直角边分别与AC、BC相交，交点分别为D、E，则CD+CE=（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{6}$ |
17．
如图，E、F、G、H分别是四边形ABCD四条边的中点，则四边形EFGH一定是（ ）
如图，E、F、G、H分别是四边形ABCD四条边的中点，则四边形EFGH一定是（ ）| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 正方形 |
7．下列各式从左到右的变形是因式分解的是（ ）
| A． | m（a+b）=ma+mb | B． | a2-a=2=a（a-1）-2 | ||
| C． | -4a2+9b2=（-2a+3b）（2a+3b） | D． | x2-$\frac{1}{{y}^{2}}$=（x-$\frac{1}{y}$）（x+$\frac{1}{y}$） |
14．实数-3，3，0，$\sqrt{2}$中最大的数是（ ）
| A． | -3 | B． | 3 | C． | 0 | D． | $\sqrt{2}$ |
11．定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（-2，-2）都是“平衡点”．当-1≤x≤3时，直线y=2x+m上有“平衡点”，则m的取值范围是（ ）
| A． | 0≤m≤1 | B． | -3≤m≤1 | C． | -3≤m≤3 | D． | -1≤m≤0 |
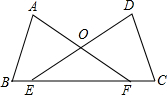如图，点B、E、F、C在同一直线上，点A、D位于BC同侧，AB=DC，BE=CF，∠B=∠C．