题目内容

8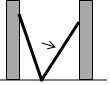．如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（　　）
A．0.7米B．1.5米C．2.2米D．2.4米

分析 先根据勾股定理求出AB的长，同理可得出BD的长，进而可得出结论．

解答 解：在Rt△ACB中，∵∠ACB=90°，BC=0.7米，AC=2.4米，
∴AB2=0.72+2.42=6.25．
在Rt△A′BD中，∵∠A′DB=90°，A′D=2米，BD2+A′D2=A′B′2，
∴BD2+22=6.25，
∴BD2=2.25，
∵BD＞0，
∴BD=1.5米，
∴CD=BC+BD=0.7+1.5=2.2米．
故选C．

点评 本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．

练习册系列答案
相关题目
18．分解因：x2-4xy-2y+x+4y2=（x-2y）（x-2y-1）．
19．方程组$\left\{\begin{array}{l}{x+1=3}\\{x+y=5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$．
16．为了解中考体育科目训练情况，某区从九年级学生中抽取了部分学生进行了一次中考体育科测试（把测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
（1）求本次抽样测试的学生人数；
（2）求图1中∠α的度数，并把图2条形统计图补充完整；
（3）该区九年级有学生4000名，如果全部参加这次体育测试，请估计不及格的人数大约是多少；
（4）测试老师想从4位同学（分别记为E、F、G、H，其中E为小明）中随机选择两位同学了解平时训练情况，请用列表或画树状图的方法求出选中小明的概率．
3．一副含30°和45°角的三角板ABC和DEF叠合在一起，边BC与EF重合，BC=EF=12cm（如图1），点G为边BC（EF）的中点，边FD与AB相交于点H，此时线段BH的长是（12$\sqrt{3}$-12）cm．现将三角板DEF绕点G按顺时针方向旋转（如图2），在∠CGF从0°到60°的变化过程中，点H相应移动的路径长共为（12$\sqrt{3}$-18）cm．（结果保留根号）
13．如图，BC∥DE，若∠A=35°，∠C=24°，则∠E等于（　　）
A．24°B．59°C．60°D．69°
20．关于$\sqrt{8}$的叙述正确的是（　　）
A．在数轴上不存在表示$\sqrt{8}$的点B．$\sqrt{8}$=$\sqrt{2}$+$\sqrt{6}$
C．$\sqrt{8}$=±2$\sqrt{2}$D．与$\sqrt{8}$最接近的整数是3
17．若1-$\sqrt{3}$是方程x2-2x+c=0的一个根，则c的值为（　　）
A．-2B．4$\sqrt{3}$-2C．3-$\sqrt{3}$D．1+$\sqrt{3}$
18．当x=1时，二次函数y=x2-2x+6有最小值5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网