当x=1时.二次函数y=x2-2x+6有最小值5．题目和参考答案——青夏教育精英家教网—

题目内容

18．当x=1时，二次函数y=x²-2x+6有最小值5．

分析把x²-2x+6化成（x-1）²+5，即可求出二次函数y=x²-2x+6的最小值是多少．

解答解：∵y=x²-2x+6=（x-1）²+5，
∴当x=1时，二次函数y=x²-2x+6有最小值5．
故答案为：1、5．

点评此题主要考查了二次函数的最值，要熟练掌握，确定一个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．

练习册系列答案

相关题目

8．

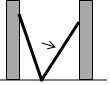如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米．如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为（　　）

9．

如图，AB为半圆O的直径，AC是⊙O的一条弦，D为$\widehat{BC}$的中点，作DE⊥AC，交AB的延长线于点F，连接DA．
（1）求证：EF为半圆O的切线；
（2）若DA=DF=6$\sqrt{3}$，求阴影区域的面积．（结果保留根号和π）

6．某市从今年1月1日起调整居民用水价格，每立方米水费上涨$\frac{1}{3}$．小丽家去年12月份的水费是15元，而今年5月的水费则是30元．已知小丽家今年5月的用水量比去年12月的用水量多5m³．求该市今年居民用水的价格．设去年居民用水价格为x元/m³，根据题意列方程，正确的是（　　）

A．

$\frac{30}{{（{1+\frac{1}{3}}）x}}-\frac{15}{x}=5$

B．

$\frac{30}{{（{1-\frac{1}{3}}）x}}-\frac{15}{x}=5$

C．

$\frac{30}{x}-\frac{15}{{（{1+\frac{1}{3}}）x}}=5$

D．

$\frac{30}{x}-\frac{15}{{（{1-\frac{1}{3}}）x}}=5$

13．计算：2017⁰-|1-$\sqrt{2}}$|+（$\frac{1}{3}}$）^-1+2cos45°．

a²+a³=a⁵

a²•a³=a⁵

（a²）³=a⁵

10．先化简，再求值：（2+x）（2-x）+（x-1）（x+5），其中x=$\frac{3}{2}$．

12．小李在某水果店里买了5kg大青枣，3kg草莓，老板少要2元，收了50元；同时小王也买了11kg大青枣，5kg草莓，老板按九折收钱，收了90元，问该店的大青枣和草莓的单价各是多少元？

13．下列图形中，既是轴对称图形又是中心对称图形的是（　　）

试题分类