题目内容
20.先阅读并填空,再解答问题:我们知道$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,那么$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,$\frac{1}{2014×2015}$=$\frac{1}{2014}$-$\frac{1}{2015}$,用含有n的式子表示你发现的规律:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,并依此计算:$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$.
分析 分子为1,分母为相邻2个自然数的分数应等于分子为1,分母分别为这两个自然数的分数的差,依此规律得到所要计算的式子的每个分数等于分子为1,分母分别为原分数中2个因数的分数的差的一半,进而化解计算即可.
解答 解:$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,
$\frac{1}{2014×2015}$=$\frac{1}{2014}$-$\frac{1}{2015}$,
$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
故答案为:$\frac{1}{4}$-$\frac{1}{5}$,$\frac{1}{2014}$-$\frac{1}{2015}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$=$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{8}$+…+$\frac{1}{2014}$-$\frac{1}{2016}$)=$\frac{1}{2}$×($\frac{1}{2}$-$\frac{1}{2016}$)=$\frac{1007}{4032}$.
点评 此题考查数的变化规律的应用;得到分子为1,分母为2个等差的数的积的分数的化简规律是解决本题的关键.

练习册系列答案
相关题目
9.某篮球队教练记录了该队一名主力前锋练习罚篮的结果如下:
(1)填表求该前锋罚篮命中的频率(保留三个有效数字);
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是什么吗?
| 练习罚球次数 | 30 | 60 | 90 | 150 | 200 | 300 | 400 | 500 |
| 罚中次数 | 27 | 45 | 78 | 118 | 161 | 239 | 322 | 401 |
| 罚中频率 |
(2)比赛中该前锋队员上篮得分并造成对手犯规,罚篮一次,你能估计这次他能罚中的概率是什么吗?
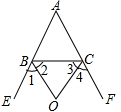 若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC.
若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=n°,画出图形并用n的代数表示∠BOC. 如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分.
如图,在平面直角坐标系中,一次函数y=-x+2的图象分别交x、y轴于点A,B,另一直线y=kx+b(k≠0)经过点C(1,0)且把△AOB的面积分成两部分.
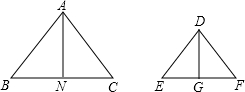 已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF.
已知:在△ABC与△DEF中,AN⊥BC于N,DG⊥EF于G,$\frac{AB}{DG}$=$\frac{AC}{DF}$=$\frac{AN}{DG}$,求证:△ABC∽△DEF.
 如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.
如图,AB为⊙O的直径,C为⊙O上一点,过C点的切线CE垂直于弦AD于点E,连OD交AC于点F.