题目内容
6.求一元一次不等式组$\left\{\begin{array}{l}{\frac{x}{3}≥-1}\\{3x+4<1}\end{array}\right.$的解集,并将解集在数轴上表示.分析 分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可;
解答 解:$\left\{\begin{array}{l}{\frac{x}{3}≥-1①}\\{3x+4<1②}\end{array}\right.$
解不等式①得 x≥-3,
解不等式②得x<-1,
所以不等式组的解集是-3≤x<-1,
解集上表示如图:
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
14.一元二次方程x2+2x-4=0的根的情况为( )
| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 无法确定 |
1.下列事件是必然事件的是( )
| A. | 若a>b,则ac<bc | |
| B. | 在常规情况下,将水加热到100℃时水会沸腾 | |
| C. | 投掷一枚硬币,落地后正面朝上 | |
| D. | 长为3cm、3cm、7cm的三条线段能围成一个三角形 |
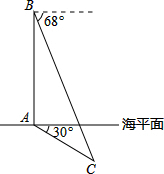 我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
我海军在我国的南海海域举行反潜实战演习.在演习过程中,如图所示,军舰A测得潜艇C的俯角为30°,在军舰A正上方1000米的反潜直升机B测得潜艇C的俯角为68°.请根据以上数据计算潜艇的下潜深度.(结果保留整数,参考数据:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5°,$\sqrt{3}$≈1.7)
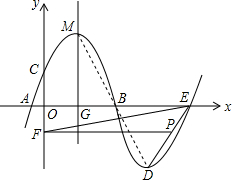 如图,抛物线m:y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4与x轴交于点A、B,顶点为M(3,$\frac{25}{4}$),将抛物线m绕点B旋转180°得到新的抛物线n,此时A点旋转至E点,M点旋转至D点.
如图,抛物线m:y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4与x轴交于点A、B,顶点为M(3,$\frac{25}{4}$),将抛物线m绕点B旋转180°得到新的抛物线n,此时A点旋转至E点,M点旋转至D点.