题目内容
18.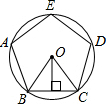 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )| A. | R2-r2=a2 | B. | a=2Rsin36° | C. | a=2rtan36° | D. | r=Rcos36° |
分析 根据圆内接正五边形的性质求出∠BOC,再根据垂径定理求出∠1=36°,然后利用勾股定理和解直角三角形对各选项分析判断即可得解.
解答  解:∵⊙O是正五边形ABCDE的外接圆,
解:∵⊙O是正五边形ABCDE的外接圆,
∴∠BOC=$\frac{1}{5}$×360°=72°,
∴∠1=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×72°=36°,
R2-r2=($\frac{1}{2}$a)2=$\frac{1}{4}$a2,
$\frac{1}{2}$a=Rsin36°,
a=2Rsin36°;
$\frac{1}{2}$a=rtan36°,
a=2rtan36°,
cos36°=$\frac{r}{R}$,
r=Rcos36°,
所以,关系式错误的是R2-r2=a2.
故选A.
点评 本题考查了圆内接四边形,解直角三角形,熟练掌握圆内接正五边形的性质并求出中心角的度数是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
6. 如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
 如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )| A. | 60m2 | B. | 63m2 | C. | 64m2 | D. | 66m2 |
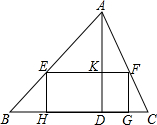 已知锐角△ABC中,边BC长为12,高AD长为8.
已知锐角△ABC中,边BC长为12,高AD长为8. 在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).
在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).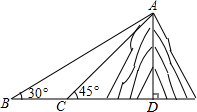 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732) 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( ) 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.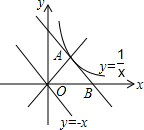 如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0).
如图,函数y=-x的图象是二、四象限的角平分线,将y=-x的图象以点O为中心旋转90°与函数y=$\frac{1}{x}$的图象交于点A,再将y=-x的图象向右平移至点A,与x轴交于点B,则点B的坐标为(2,0).