题目内容
3.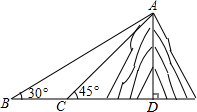 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为137米(结果保留整数,测角仪忽略不计,$\sqrt{2}$≈1.414,$\sqrt{3}$,1.732)
分析 根据仰角和俯角的定义得到∠ABD=30°,∠ACD=45°,设AD=xm,先在Rt△ACD中,利用∠ACD的正切可得CD=AD=x,则BD=BC+CD=x+100,然后在Rt△ABD中,利用∠ABD的正切得到x=$\frac{\sqrt{3}}{3}$(x+100),解得x=50($\sqrt{3}$+1),再进行近似计算即可.
解答 解:如图,∠ABD=30°,∠ACD=45°,BC=100m,
设AD=xm,
在Rt△ACD中,∵tan∠ACD=$\frac{AD}{CD}$,
∴CD=AD=x,
∴BD=BC+CD=x+100,
在Rt△ABD中,∵tan∠ABD=$\frac{AD}{BD}$,
∴x=$\frac{\sqrt{3}}{3}$(x+100),
∴x=50($\sqrt{3}$+1)≈137,
即山高AD为137米.
故答案为137.
点评 本题考查了解直角三角形-的应用-仰角俯角:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
11.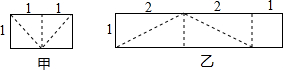 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
 如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )| A. | 甲、乙都可以 | B. | 甲、乙都不可以 | C. | 甲不可以、乙可以 | D. | 甲可以、乙不可以 |
18.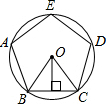 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )| A. | R2-r2=a2 | B. | a=2Rsin36° | C. | a=2rtan36° | D. | r=Rcos36° |
12. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
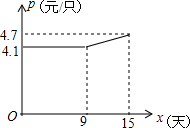 某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元.为按时完成任务,该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只,y与x满足如下关系:y=$\left\{\begin{array}{l}{54x(0≤x≤5)}\\{30x+120(5<x≤15)}\end{array}\right.$
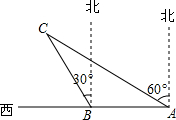 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732)
如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732) 点A,B在数轴上的位置如图所示,点P是数轴上的一动点.
点A,B在数轴上的位置如图所示,点P是数轴上的一动点.