题目内容
20.计算:(1)$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$;
(2)$(2+\sqrt{3}-\sqrt{5})(2-\sqrt{3}+\sqrt{5})$.
分析 (1)先进行二次根式的乘除运算,然后化简后合并即可;
(2)先变形得到原式=[2+(3-$\sqrt{5}$)][2-(3-$\sqrt{5}$)],然后利用平方差公式和完全平方公式计算即可.
解答 解:(1)原式=$\sqrt{48÷3}$-$\sqrt{\frac{1}{2}×12}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=4+$\sqrt{6}$;
(2)原式=[2+(3-$\sqrt{5}$)][2-(3-$\sqrt{5}$)]
=22-(3-$\sqrt{5}$)2
=4-(9-6$\sqrt{5}$+5)
=4-14+6$\sqrt{5}$
=-10+6$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
10. 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )| A. | -1≤b≤$\frac{1}{2}$ | B. | -1≤b≤1 | C. | -$\frac{1}{2}$≤b≤1 | D. | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
5.小李将1000元钱存入银行,年利率为x,第二年他把本息和全部存入银行,两年后不计利息税,他得到本息共a元,则依题意可列方程为( )
| A. | 1000(x+x)=a | B. | 1000(1-2x)=a | C. | 1000(1+x)2=a | D. | 1000(1+2x)2=a |
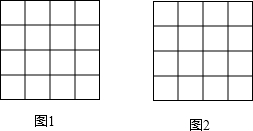 如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点. 阅读下列材料:已知,$\sqrt{2^2}=2$,$\sqrt{{{({-2})}^2}}=2$,$\sqrt{3^2}=3$,$\sqrt{{{({-3})}^2}}=3$,$\sqrt{4^2}=4$,$\sqrt{{{({-4})}^2}}=4$,$\sqrt{0^2}=0$,…
阅读下列材料:已知,$\sqrt{2^2}=2$,$\sqrt{{{({-2})}^2}}=2$,$\sqrt{3^2}=3$,$\sqrt{{{({-3})}^2}}=3$,$\sqrt{4^2}=4$,$\sqrt{{{({-4})}^2}}=4$,$\sqrt{0^2}=0$,…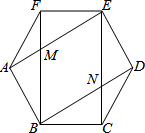 如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.