题目内容
19.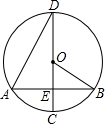 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.(1)求∠BOC的度数;
(2)求CE的长.
分析 (1)先根据垂径定理得出$\widehat{AC}$=$\widehat{BC}$,再由∠ADC=30°求出∠BOC的度数即可;
(2)在Rt△OBE中,根据BE=$\sqrt{3}$,∠BOC=60°可得出OB及OE的长,进而可得出CE的长.
解答 解:(1)∵弦AB垂直于直径CD,∠ADC=30°,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠BOC=2∠ADC=60°;
(2)∵AB⊥CD,AB=2$\sqrt{3}$,
∴BE=$\frac{1}{2}$AB=$\sqrt{3}$.
∵由(1)知,∠BOC=60°,
∴OB=$\frac{BE}{sin60°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,OE=$\frac{BE}{tan60°}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1,
∴CE=2-1=1.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.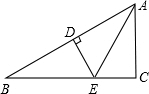 如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )
如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )
 如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )
如图,AB的垂直平分线交AB于D,交BC于E,AE平分∠BAC,∠B=30°,DE=2cm,则BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
7.下列数中,是有理数的是( )
| A. | π | B. | (-2$\sqrt{3}$)2 | C. | $\sqrt{2}$ | D. | $\root{3}{9}$ |
4.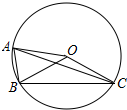 如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )
如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )
 如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )
如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )| A. | 120° | B. | 80° | C. | 60° | D. | 30° |
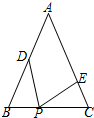 如图,△ABC中,AB=AC,∠A=50°,BP=CE,BD=CP,∠DPE的度数是65°.
如图,△ABC中,AB=AC,∠A=50°,BP=CE,BD=CP,∠DPE的度数是65°.