题目内容
4.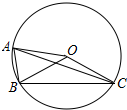 如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )
如图,⊙O是△ABC的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC的度数是( )| A. | 120° | B. | 80° | C. | 60° | D. | 30° |
分析 由∠ACB=20°,根据同弧所对的圆周角等于圆心角的一半,可得∠AOB=2∠ACB=40°,然后由,∠BOC=3∠AOB,可求∠BOC=120°,最后再根据同弧所对的圆周角等于圆心角的一半,可得∠BAC=$\frac{1}{2}$∠BOC=60°.
解答 解:∵∠ACB=20°,
∴∠AOB=2∠ACB=40°,
∵∠BOC=3∠AOB,
∴∠BOC=120°,
∴∠BAC=$\frac{1}{2}$∠BOC=60°.
故选C.
点评 此题主要考查了圆周角定理,题目比较基础,关键是找准同弧所对的圆周角与圆心角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )
 下列选项中能由左图平移得到的是( )
下列选项中能由左图平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
9.若a>b,则下列各式中一定成立的是( )
| A. | $\frac{a}{2}$<$\frac{b}{2}$ | B. | am>bm | C. | a+2>b+2 | D. | -a>-b |
16. 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
 如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )
如图所示,直线a∥b,AB⊥直线a,BC与直线b相交于点D,若∠1=43°,则∠2的度数是( )| A. | 43° | B. | 47° | C. | 120° | D. | 133° |
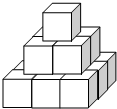 如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.
如图把14个棱长为1分米的正方体摆放在课桌上,现在想露出的表面都涂上颜色,则涂上颜色部分的面积为33平方分米.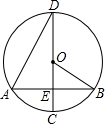 如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.
如图,在⊙O中,弦AB垂直于直径CD,垂足为E,连接OB、AD,∠ADC=30°,弦AB=2$\sqrt{3}$.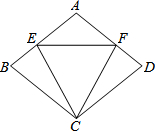 如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.
如图,等腰△CEF的两腰CE、CF的长与菱形ABCD的边长相等.